Fibonacci numbers
Fibonacci numbers is a numerical sequence, in which first two elements are equal to 1, and each remaining number is equal to the sum of the previous two: F(1) = F(2) = 1, F(n) = F(n-1) + F(n-2).
(Note that this is different than the traditional definition of the Fibonacci function, where F(0) = F(1) = 1, but it doesn’t really matter, as the output is the same.)
The task is to output first 16 Fibonacci numbers in the following format:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
Note that this example can be implemented in several ways:
- using the recurrence equation itself. The least efficient way which illustrates the usage of recurrent functions.
- saving calculated numbers in an array. Illustrates the usage of arrays.
- using Binet’s formula. Illustrates the usage of math functions.
Example for versions Borland C++ Builder 6, g++ 3.4.5, Microsoft Visual C++ 6, Microsoft Visual C++ 9 (2008)
This example uses recursive definition of Fibonacci numbers.
#include <iostream>
int fibonacci(int n)
{
return ( n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2) );
}
int main(void)
{
for (int n=1; n<=16; n++)
std::cout << fibonacci(n) << ", ";
std::cout << "..." << std::endl;
return 0;
}
Example for versions gcj 3.4.5, Groovy 1.7, Sun Java 6
This example uses recursive definition of Fibonacci numbers.
public class Fibonacci {
static int fibonacci(int n)
{
return (n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2));
}
public static void main(String[] args)
{
for (int n=1; n<=16; n++)
System.out.print(fibonacci(n)+", ");
System.out.println("...");
}
}
Example for versions Oracle 10g SQL, Oracle 11g SQL
Pure SQL doesn’t support loops, recursions or user-defined functions. Besides, concatenating fields from multiple rows of a table or a subquery is not a standard aggregate function. This example uses:
-
Binet’s formula and math functions
round,powerandsqrtto calculate n-th Fibonacci number; - pseudocolumn level to construct a pseudotable t1 containing numbers 1 through 16;
-
built-in function
SYS_CONNECT_BY_PATHto concatenate the resulting numbers in ascending order.
SELECT REPLACE(MAX(SYS_CONNECT_BY_PATH(fib||', ', '/')),'/','')||'...' fiblist
FROM (
SELECT n, fib, ROW_NUMBER()
OVER (ORDER BY n) r
FROM (select n, round((power((1+sqrt(5))*0.5, n)-power((1-sqrt(5))*0.5, n))/sqrt(5)) fib
from (select level n
from dual
connect by level <= 16) t1) t2
)
START WITH r=1
CONNECT BY PRIOR r = r-1;
Example for versions EsCo 0.511 (Brainfuck), Müller's Brainfuck 2.0
This example uses iterative definition of Fibonacci numbers. A high-level description of what it does is: store two last numbers in variables c4 and c5 (initially c4=0, c5=1), print the number stored in c5 (this operation takes the major part of the code), calculate next number (c6 = c5+c4), and move the numbers sequence one number back (c4 = c5, c5 = c6). A low-level description is given in the comments, notation “cXvY” meaning that after execution of the commands in the line the data pointer is at cell X, and the value at this cell is Y. A total of 12 memory cells is used.
This example uses one minor cheat: classic Brainfuck interpreter uses byte variables to store values of memory cells, so Fibonacci numbers 14 through 16 will cause overflow. Writing long arithmetics in Brainfuck is a bit of overkill, so in this example we assume that memory cells can store integer values.
++++++++++++++++++++++++++++++++++++++++++++ c1v44 : ASCII code of comma
>++++++++++++++++++++++++++++++++ c2v32 : ASCII code of space
>++++++++++++++++ c3v11 : quantity of numbers to be calculated
> c4v0 : zeroth Fibonacci number (will not be printed)
>+ c5v1 : first Fibonacci number
<< c3 : loop counter
[ block : loop to print (i)th number and calculate next one
>> c5 : the number to be printed
block : divide c5 by 10 (preserve c5)
> c6v0 : service zero
>++++++++++ c7v10 : divisor
<< c5 : back to dividend
[->+>-[>+>>]>[+[-<+>]>+>>]<<<<<<] c5v0 : divmod algo; results in 0 n d_n%d n%d n/d
>[<+>-] c5 : move dividend back to c5 and clear c6
>[-] c7v0 : clear c7
>> block : c9 can have two digits; divide it by ten again
>++++++++++ c10v10: divisor
< c9 : back to dividend
[->-[>+>>]>[+[-<+>]>+>>]<<<<<] c9v0 : another divmod algo; results in 0 d_n%d n%d n/d
>[-] c10v0 : clear c10
>>[++++++++++++++++++++++++++++++++++++++++++++++++.[-]]c12v0 : print nonzero n/d (first digit) and clear c12
<[++++++++++++++++++++++++++++++++++++++++++++++++.[-]] c11v0 : print nonzero n%d (second digit) and clear c11
<<<++++++++++++++++++++++++++++++++++++++++++++++++.[-] c8v0 : print any n%d (last digit) and clear c8
<<<<<<<.>. c1c2 : print comma and space
block : actually calculate next Fibonacci in c6
>>[>>+<<-] c4v0 : move c4 to c6 (don't need to preserve it)
>[>+<<+>-] c5v0 : move c5 to c6 and c4 (need to preserve it)
>[<+>-] c6v0 : move c6 with sum to c5
<<<- c3 : decrement loop counter
]
<<++... c1 : output three dots
Example for versions Microsoft SQL Server 2005, Microsoft SQL Server 2008 R2, Microsoft SQL Server 2012
This example uses a kind of iterative definition of Fibonacci numbers, implemented with a recursive query. Each row of recursive query contains two consecutive numbers of the sequence, and next row is calculated as (last number, sum of numbers) of previous row. This way most numbers are stored twice, so only first number of each row is included in the result.
with fibonacci(a, b) as
(
select 1, 1
union all
select b, a+b from fibonacci where b < 1000
)
SELECT cast(a as varchar)+', ' AS [text()]
FROM fibonacci
FOR XML PATH ('')
Example for versions Interactive FP
This example works in a same way as the factorial one, but without readability functions added.
{ seq ( = @ [id, %1] -> %<1> ; concat @ [ seq @ - @ [id, %1] , [id] ] ) }
{ fibonacci ( < @ [id, %3] -> %1 ; + @ [ fibonacci @ - @ [id, %1], fibonacci @ - @ [id, %2] ] ) }
&fibonacci @ seq:16
Example for versions clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
This example uses recursive definition of Fibonacci numbers and expands use of loop macro to finally clause (expression evaluated after the loop is done).
(defun fibonacci (n)
(if (< n 3)
1
(+ (fibonacci (- n 1)) (fibonacci (- n 2))) ) )
(loop for i from 1 to 16
do (format t "~D, " (fibonacci i))
finally (format t "...~%") )
Example for versions clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6
This example uses iterative definition of Fibonacci numbers, though expressed through recursive calls of fib-iter.
(defun fibonacci (n)
(defun fib-iter (a b count)
(if (zerop count)
b
(fib-iter (+ a b) a (- count 1)) ) )
(fib-iter 1 0 n) )
(loop for i from 1 to 16
do (format t "~D, " (fibonacci i))
finally (format t "...~%") )
Example for versions Microsoft Visual Basic 6
This example uses recursive definition of Fibonacci numbers.
Option Explicit
Declare Function AllocConsole Lib "kernel32" () As Long
Declare Function FreeConsole Lib "kernel32" () As Long
Declare Function CloseHandle Lib "kernel32" (ByVal hObject As Long) As Long
Declare Function GetStdHandle Lib "kernel32" (ByVal nStdHandle As Long) As Long
Declare Function WriteConsole Lib "kernel32" Alias "WriteConsoleA" _
(ByVal hConsoleOutput As Long, lpBuffer As Any, ByVal _
nNumberOfCharsToWrite As Long, lpNumberOfCharsWritten As Long, _
lpReserved As Any) As Long
Declare Function Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) As Long
Public Function Fibonacci(ByVal n As Integer) As Integer
If (n <= 2) Then
Fibonacci = 1
Else
Fibonacci = Fibonacci(n - 1) + Fibonacci(n - 2)
End If
End Function
Private Sub Main()
'create a console instance
AllocConsole
'get handle of console output
Dim hOut As Long
hOut = GetStdHandle(-11&)
'output string to console output
Dim s As String
Dim i As Integer
For i = 1 To 16 Step 1
s = Fibonacci(i) & ", "
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
Next i
s = "..." & vbCrLf
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
'make a pause to look at the output
Sleep 2000
'close the handle and destroy the console
CloseHandle hOut
FreeConsole
End Sub
Example for versions QBasic 1.1, QuickBASIC 4.5
Numbers which have already been calculated are stored in array F and are retrieved from it to calculate the next ones. To get program output in required format, the numbers in the array are concatenated to form one string with required delimiters. STR$ function converts a number to a string.
DIM F(16)
F(1) = 1
F(2) = 1
FOR i = 3 TO 16:
F(i) = F(i - 1) + F(i - 2)
NEXT i
DIM S AS STRING
S = ""
FOR i = 1 TO 16:
S = S + STR$(F(i)) + ", "
NEXT i
S = S + "..."
PRINT S
Example for versions QBasic 1.1, QuickBASIC 4.5
This example uses recursive definition of Fibonacci numbers. Each call of PRINT function prints the arguments to a separate line and adds a space before and after printed number, so program output looks like this:
1 ,
1 ,
2 ,
3 ,
5 ,
8 ,
13 ,
21 ,
34 ,
55 ,
89 ,
144 ,
233 ,
377 ,
610 ,
987 ,
…
DECLARE FUNCTION fibonacci (n)
FOR i = 1 TO 16:
PRINT fibonacci(i); ", "
NEXT i
PRINT "..."
FUNCTION fibonacci (n)
IF (n <= 2) THEN
fibonacci = 1
ELSE
fibonacci = fibonacci(n - 1) + fibonacci(n - 2)
END IF
END FUNCTION
Example for versions QBasic 1.1, QuickBASIC 4.5
Fibonacci numbers are calculated using Binet’s formula. The resulting numbers can differ from actual ones slightly due to calculation imprecision; to remove this effect, we use function INT which truncates fractional part of the number.
DECLARE FUNCTION FIBONACCI (n)
DIM S AS STRING
S = ""
FOR i = 1 TO 16:
S = S + STR$(INT(FIBONACCI(i) + .1)) + ","
NEXT i
S = S + "..."
PRINT S
FUNCTION FIBONACCI (n)
p1 = ((1 + SQR(5)) * .5) ^ n
p2 = ((1 - SQR(5)) * .5) ^ n
FIBONACCI = (p1 - p2) / SQR(5)
END FUNCTION
Example for versions Lua 5.0.3
This example uses recursive definition of Fibonacci numbers.
function fibonacci(n)
if n<3 then
return 1
else
return fibonacci(n-1) + fibonacci(n-2)
end
end
for n = 1, 16 do
io.write(fibonacci(n), ", ")
end
io.write("...\n")
Example for versions Lua 5.0.3
Numbers which have already been calculated are stored in associative array fib and are retrieved from it to calculate the next ones. By default Lua associative arrays use 1-based integer keys, so fib = {1, 1} creates an array with indices 1 and 2.
fib = {1, 1}
for n = 3, 16 do
fib[n] = fib[n-1] + fib[n-2]
end
for n = 1, 16 do
io.write(fib[n], ", ")
end
io.write("...\n")
Example for versions Visual Prolog 7.2
Create a new project with UI Strategy “Console” and replace contents of files main.cl and main.pro with given code.
Here we define two new predicates — fibonacci(N,F) to calculate Nth Fibonacci number and loop(N) to output it. We don’t use memoization to store already calculated numbers, so this implementation is rather inefficient. Note the way the predicates are defined — each predicate is written as one clause using conjunction , and disjunction ; of elementary predicates (instead of breaking them in several clauses which use only disjunction).
% main.cl
class main
open core
predicates
classInfo : core::classInfo.
fibonacci : (integer N, integer F) procedure (i,o).
loop : (integer N) procedure (i).
predicates
run : core::runnable.
end class main
% main.pro
implement main
open core
constants
className = "main".
classVersion = "".
clauses
classInfo(className, classVersion).
fibonacci(N,F) :-
N < 3, !, F = 1;
fibonacci(N-1,F1), fibonacci(N-2,F2), F = F1 + F2.
loop(N) :-
( N = 1, !, fibonacci(1,F);
loop(N-1), fibonacci(N,F) ),
stdio::write(F, ", ").
clauses
run():-
console::init(),
loop(16),
stdio::write("..."),
programControl::sleep(1000),
succeed().
end implement main
goal
mainExe::run(main::run).
Example for versions Oracle 10g SQL, Oracle 11g SQL
This example shows the use of model clause, available since Oracle 10g. It allows array-like processing of query rows. Each row has two columns — Fibonacci number itself (stored in f) and concatenation of all Fibonacci numbers less than or equal to the current Fibonacci number (stored in s). Iterative aggregation of Fibonacci numbers in the same query that they were generated is easier than aggregating them separately.
select max(s) || ', ...'
from
(select s
from dual
model
return all rows
dimension by ( 0 d )
measures ( cast(' ' as varchar2(200)) s, 0 f)
rules iterate (16)
( f[iteration_number] = decode(iteration_number, 0, 1, 1, 1, f[iteration_number-1] + f[iteration_number-2]),
s[iteration_number] = decode(iteration_number, 0, to_char(f[iteration_number]), s[iteration_number-1] || ', ' || to_char(f[iteration_number]))
)
);
Example for versions MySQL 3.23.57
Replace TABLE with name of any table you have access to, like mysql.help_topic.
select concat(group_concat(f separator ', '), ', ...')
from (select @f := @i + @j as f, @i := @j, @j := @f
from TABLE, (select @i := 1, @j := 0) sel1
limit 16) t
Example for versions Poplog 15.5 (Prolog)
Straightforward recursive implementation is too memory inefficient to be executed in Poplog, so this example shows a more advanced technique — recursion with memoization. An additional predicate memo(Goal) is defined so that the first time Goal is evaluated, the result of its evaluation is added to facts database, and next time it is questioned, it is not re-evaluated but taken as a known fact.
After this predicate fib(N,F) is defined recursively, but each call to fib is wrapped in memo, so for each value of N fib(N,F) is evaluated only once. With such approach printing calculated numbers can be done immediately after their calculation, without extra loop.
% fibonacci.pl
:- dynamic(stored/1).
memo(Goal) :-
stored(Goal) -> true;
Goal, assertz(stored(Goal)).
fib(1,1) :- !, write('1, ').
fib(2,1) :- !, write('1, ').
fib(N,F) :-
N1 is N-1, memo(fib(N1,F1)),
N2 is N-2, memo(fib(N2,F2)),
F is F1 + F2,
write(F), write(', ').
% interactive
[-fibonacci].
fib(16,X), write('...'), nl.
Example for versions Free Pascal 2.0.4, Free Pascal 2.2.0, gpc 20070904, Turbo Pascal 1.0, Turbo Pascal 2.0, Turbo Pascal 3.0, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 5.5, Turbo Pascal 6.0, Turbo Pascal 7.0
This example uses recursive definition of Fibonacci numbers.
program fibonacci;
function fib(n:integer): integer;
begin
if (n <= 2) then
fib := 1
else
fib := fib(n-1) + fib(n-2);
end;
var
i:integer;
begin
for i := 1 to 16 do
write(fib(i), ', ');
writeln('...');
end.
Example for versions ARIBAS 1.53
This example uses recursive definition of Fibonacci numbers.
ARIBAS uses integer type for variables by default, so type declaration can be omitted.
group(0) is used to cancel digit groups separation by underscores during output.
function fib(n);
begin
if (n < 3) then
return(1);
end;
return(fib(n-1)+fib(n-2));
end;
function fib1_16();
var n;
begin
for n := 1 to 16 do
write(fib(n): group(0), ", ");
end;
writeln("...");
end;
fib1_16().
Example for versions Python 2.5.2, Python 2.6.5
This example uses recursive definition of Fibonacci numbers.
#! /usr/bin/env python
def fibonacci(n):
if n < 3:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
for n in range(1, 16 + 1):
print "%i," % fibonacci(n) ,
print "..."
Example for versions Microsoft Visual Basic .NET 9 (2008), vbnc 2.4.2
This example uses recursive definition of Fibonacci numbers.
Module Module1
Function Fibonacci(ByVal n As Integer) As Long
If n < 3 Then
Return 1
Else
Return Fibonacci(n - 1) + Fibonacci(n - 2)
End If
End Function
Sub Main()
For i As Integer = 1 To 16
Console.Write(Fibonacci(i) & ", ")
Next
Console.WriteLine("...")
End Sub
End Module
Example for versions gmcs 2.0.1, Microsoft Visual C# 2008
This example uses recursive definition of Fibonacci numbers.
using System;
class Program
{
static long Fibonacci(int n)
{
if (n < 3)
return 1;
else
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
static void Main(string[] args)
{
for (int i = 1; i < 17; i++)
Console.Write("{0}, ", Fibonacci(i));
Console.WriteLine("...");
}
}
Example for versions PHP 5.2.4, PHP 5.3.2
This example uses recursive definition of Fibonacci numbers.
<?php
function fibonacci($n)
{
if ($n < 3) {
return 1;
}
return fibonacci($n-1) + fibonacci($n-2);
}
for ($n = 1; $n <= 16; $n++) {
echo fibonacci($n) . ", ";
}
echo "...\n";
?>
Example for versions Poplog 15.5 (POP-11)
This example uses recursive definition of Fibonacci numbers and works in the same way as factorial example, except for that loop returns a string which contains a concatenation of all Fibonacci numbers up to n-th.
define fibonacci(n);
if n < 3
then 1
else fibonacci(n - 1) + fibonacci(n - 2)
endif
enddefine;
define loop(n);
if n>1
then loop(n-1) >< ', ' >< fibonacci(n)
else fibonacci(n)
endif;
enddefine;
loop(16) >< ', ...' =>
Example for versions Perl 6 (alpha), rakudo-2010.08
Not the shortest possible implementation, but perhaps the easiest to read and understand.
sub fib { 1,1, {$^x + $^y} ... * }
fib[^16], '...' ==> join(', ') ==> say;
Example for versions Euphoria v3.1.1, Euphoria v4
This example uses recursive definition of Fibonacci numbers.
function fibonacci(integer n)
atom result = 1
if n <= 2 then
result = 1
else
result = fibonacci(n-1) + fibonacci(n-2)
end if
return result
end function
for i = 1 to 16 do
printf(1, "%d, ", fibonacci(i))
end for
puts(1, "...\n")
Example for versions Euphoria v3.1.1, Euphoria v4
This example uses iterative definition of Fibonacci numbers.
function fibonacci(integer n)
sequence result
result = repeat(1, n)
for i = 3 to n do
result[i] = result[i-1] + result[i-2]
end for
return result
end function
sequence ans = fibonacci(16)
for i = 1 to length(ans) do
printf(1, "%d, ", ans[i])
end for
puts(1, "...\n")
Example for versions Oracle 10g SQL, Oracle 11g SQL
This example implements iterative definition of Fibonacci numbers by means of PL/SQL. Already calculated numbers are stored in varray, PL/SQL analogue of array in other languages.
declare
type vector is varray(16) of number;
fib vector := vector();
i number;
s varchar2(100);
begin
fib.extend(16);
fib(1) := 1;
fib(2) := 1;
s := fib(1) || ', ' || fib(2) || ', ';
for i in 3..16 loop
fib(i) := fib(i-1) + fib(i-2);
s := s || fib(i) || ', ';
end loop;
dbms_output.put_line(s || '...');
end;
Example for versions Squeak 3.10
This code is a method of an object, and adds n Fibonacci numbers to an OrderedCollection called numbers.
Variable declarations are enclosed in vertical bars and don’t specify their type. Code blocks are enclosed in square brackets. The “^” carrot at the end returns the result from this method.
fibonacci: n
| numbers a b |
numbers := OrderedCollection new.
a := 1.
b := 1.
[ numbers size < n ] whileTrue: [
| temp |
numbers add: a.
temp := b.
b := a + b.
a := temp.
].
^ numbers.
Example for versions Squeak 3.10
This is a recursive method implementing the Fibonacci sequence, writing it to the given stream of numbers.
To invoke this method:
stream := WriteStream on: (Array new: 100). Fibonacci new fibonacci: 1 and: 1 writeTo: stream
There is no halting condition; the program will continue writing Fibonacci numbers until interrupted.
This example is far from optimal: the stream will automatically double the size of the array each time it is filled (a very expensive operation in Squeak), and the recursion continually consumes memory. The alternative iterative example is much more efficient.
fibonacci: n1 and: n2 writeTo: stream
stream nextPut: n1.
self fibonacci: n2 and: (n1+n2) writeTo: stream.
Example for versions REXX
This example uses recursive definition of Fibonacci numbers.
1 #!/usr/bin/rexx
2 /* Calculate Fibonacci using recursion */
3
4 numbers = ''
5
6 do n = 1 to 16
7 numbers = numbers fibonacci(n)","
8 end
9
10 say numbers"..."
11 exit
12
13 fibonacci: procedure
14 parse arg n .
15
16 if n < 3 then
17 n = 1
18
19 else
20 n = fibonacci(n-1) + fibonacci(n-2)
21 return n
Example for versions REXX
This example uses iterative definition of Fibonacci numbers.
In REXX, an uninitialized variable has its name in uppercase as its value; e.g. numbers = ‘NUMBERS’
Line 4: Arrays are called “stem variables”. The root of a stem ends with a period. Elements of a stem are named by adding a value to the stem; e.g. fib.1, fib.first, etc. Additional dimensions may be used by adding another period and value; e.g., fib.1.3; To initialize all possible stem instances, assign a value to the stem name; e.g., fib. = 0 or fib. = ”
1 #!/usr/bin/rexx
2 /* Calculate Fibonacci using an associative array */
3
4 fib. = ''
5 fib.1 = 1
6 fib.2 = 1
7 numbers = ''
8
9 do f = 3 to 16
10 e = f - 1; d = f - 2
11 fib.f = fib.e + fib.d
12 end
13
14 do n = 1 to 16
15 numbers = numbers fib.n','
16 fib.f = fib.e + fib.d
17 end
18
19 say numbers"..."
20 exit
Example for versions D1, D2, gdc 0.24
This example uses iterative definition of Fibonacci numbers.
module fibonacci;
import std.stdio;
ulong iterative(ulong x)
{
ulong prev1 = 1L;
ulong prev2 = 1L;
ulong result = x <= 2 ? 1L : 0L;
for ( ulong i = 3; i <= x; ++i )
{
result = prev1 + prev2;
prev1 = prev2;
prev2 = result;
}
return result;
}
int main()
{
for (uint i = 1; i < 17; i++)
{
writef("%s, ", iterative(i));
}
writefln("%s", "...");
return 0;
}
Example for versions D1, D2, gdc 0.24
This example uses recursive definition of Fibonacci numbers.
module fibonacci;
import std.stdio;
ulong recursive(ulong x)
{
return x <= 2 ? 1 : recursive( x - 2 ) + recursive( x - 1 );
}
int main()
{
for (uint i = 1; i < 17; i++)
{
writef("%s, ", recursive(i));
}
writefln("%s", "...");
return 0;
}
Example for versions j602
This example uses the recursive definition of Fibonacci numbers. @.(agenda) is a higher order dyadic function taking an array of functions(a gerund, created by tying together individual functions using the tie conjunction represented by a back-tick character) on the left and a function on the right that computes the index of the function in the function array(gerund) to be applied on the called argument.
The general call to agenda:
f1`f2@.g x
The function g is used to calculate an index using the argument x, this index is then used to select the function to be applied from the left argument of agenda, the function array. The function that is selected is then applied to the original argument x.
In the case of the above Fibonacci function, applying the semantics of the agenda function we get a function which checks whether its argument is less than two, if it is then 1 is returned otherwise the formal recursive calculation of the Fibonacci number is called on the argument.
load 'printf'
fibr=: 1:`(-&2 +&$: -&1)@.(2&<)"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibr >: i.16
Example for versions j602
This example uses iterative definition of Fibonacci numbers.
load 'printf'
fibi=: 3 : '(,+/@(_2&{.))^:y(0 1)'
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf }.fibi 15
Example for versions j602
This example uses Binet’s formula.
g =: -: >: %:5 is equivalent to g =: 0.5 * (1 + 5 ^ 0.5) and assigns name g to value of golden ratio. %: extracts square root of the number, >: increments the number, -: divides the number by two. Operations are done from right to left, unless there are no parenthesis in the formula.
fibb=: (%:5) %~ g&^ -- (1-g)&^ is equivalent to fibb =: (0.2 ^ 0.5) * (g &^ -- (1-g) &^); this defines a formula for F(n) given the value of n. %~ is division, with dividend and divisor swapped.
i.16 generates numbers from 0 to 15, inclusive.
load 'printf'
g=: -: >: %:5
fibb=: (%:5) %~ g&^ - (1-g)&^
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibb 1+i.16
Example for versions gfortran 4.5.0, Intel Visual Fortran 11.1
This example uses iterative definition of Fibonacci numbers. The tricky part is printing the calculated values in one line, without leading or trailing spaces. Format specifier (I3, A, $) means that first an integer is printed using exactly 3 positions, followed by a string. The final $ suppresses trailing carriage return, used by default, so that everything is printed in one line.
program Fibonacci
integer :: f1,f2,f3,i
i = 1
f1 = 0
f2 = 1
do
f3 = f2 + f1
f1 = f2
f2 = f3
i = i + 1
if (f1<10) then
print '(I1, A, $)', f1, ', '
elseif (f1<100) then
print '(I2, A, $)', f1, ', '
else
print '(I3, A, $)', f1, ', '
end if
if (i==17) then
exit
end if
end do
print *, '...'
end program Fibonacci
Example for versions SpiderMonkey 1.7
This example uses recursive definition of Fibonacci numbers and is meant to be executed from web-browser.
function fibonacci(n)
{ if (n<3)
return 1;
else
return fibonacci(n-1) + fibonacci(n-2);
}
var i;
document.clear();
for (i = 1; i <= 16; i++)
document.write(fibonacci(i) + ", ");
document.write("...<br />");
Example for versions GHC 6.10.4
This example uses one of the main Haskell features — lazy evaluations and infinite lists. Infinite list of Fibonacci numbers fibs is defined using zipWith function which applies its first argument (a function of two variables, in this case +) to pairs of corresponding elements of second and third arguments (lists). tail fibs returns tail of the list fibs (i.e., all elements except for the first one). Thus first element of the list returned by zipWith is a sum of first and second elements of list fibs and becomes its third element.
module Main where
import Text.Printf
fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
line n = printf "%d, " $ fibs !! n
main = do
sequence_ $ map line [1..16]
putStrLn "..."
Example for versions GHC 6.10.4
This example uses recursive definition of Fibonacci numbers via pairs of adjacent numbers in the sequence. Only first elements of the pairs are printed.
module Main where
import Text.Printf
fibNextPair :: (Int, Int) -> (Int, Int)
fibNextPair (x, y) = (y, x+y)
fibPair :: Int -> (Int, Int)
fibPair n
| n == 1 = (1, 1)
| otherwise = fibNextPair (fibPair (n-1))
line n = printf "%d, " $ (fst.fibPair) n
main = do
sequence_ $ map line [1..16]
putStrLn "..."
Example for versions gcc 3.4.5, gcc 3.4.5 (Objective-C), tcc 0.9.25
This example uses recursive definition of Fibonacci numbers. Note the difference from C++ example: loop counter must be declared outside of the loop, and printf is used for output instead of std::cout.
#include <stdio.h>
int fibonacci(int n)
{
return ( n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2) );
}
int main(void)
{
int n;
for (n=1; n<=16; n++)
printf("%d, ", fibonacci(n));
printf("...\n");
return 0;
}
Example for versions Furry Paws
This example works exactly like the one for Interactive FP.
one = eq.[id, ~1]
dec = sub.[id, ~1]
seq = one -> [~1] ; cat.[seq.dec, [id]]
fibonacci = lt.[id, ~3] -> ~1 ; add.[fibonacci.sub.[id, ~1], fibonacci.sub.[id, ~2]]
main = show.(return @fibonacci.(seq.~16))
Example for versions gnat 3.4.5, gnat 4.3.2
This example uses recursive definition of Fibonacci numbers.
with Ada.Text_IO, Ada.Integer_Text_IO;
procedure Fibonacci is
begin
declare
function Fib (N: Integer) return Integer is
begin
if N<3 then
return 1;
else
return Fib(N-1) + Fib(N-2);
end if;
end Fib;
i: Integer := 1;
begin
loop
Ada.Integer_Text_IO.Put (Item => Fib(i), Width => 1);
Ada.Text_IO.Put (", ");
i := i + 1;
exit when i=17;
end loop;
Ada.Text_IO.Put ("...");
end;
end Fibonacci;
Example for versions Scratch 1.4
This example uses recursive definition of Fibonacci numbers, since Scratch doesn’t have an easy way to define a function. Besides, Scratch is a graphical language, the print-screen contains the actual information about the program, source text is only a transcription.
set f1 to 1
set f2 to 1
set str to f1
repeat 15
set f3 to (f1 + f2)
set f1 to f2
set f2 to f3
set str to join (str (join (,) f1))
say join (str (...))
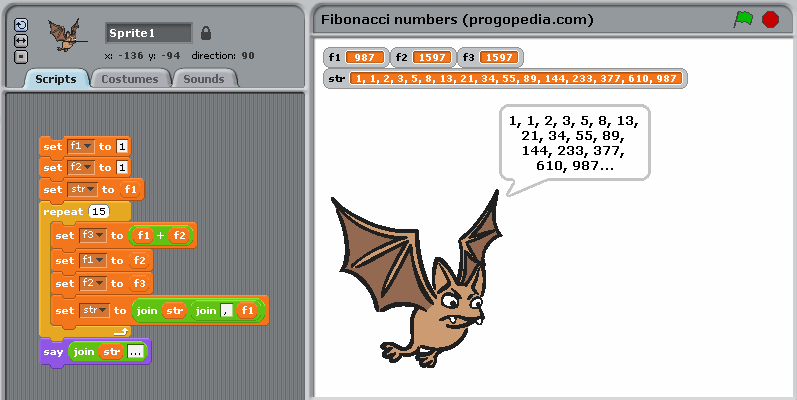
Fibonacci numbers example in Scratch
Example for versions UCBLogo 6.0
This example uses recursive definition of Fibonacci numbers. It defines two functions — fibonacci which calculates the value of Nth Fibonacci number and print_fibonacci which accumulates the numbers in a string and prints them.
to fibonacci :N
ifelse :N < 3 [output 1] [output sum fibonacci :N - 1 fibonacci :N - 2]
end
to print_fibonacci :i :N
make "str fibonacci :i
make "i sum :i 1
make "comma ",
repeat :N - :i + 1 [make "str (word :str :comma fibonacci :i)
make "i sum :i 1]
make "str word str ",...
print str
end
print_fibonacci 1 16
Example for versions gc-2010-07-14
This example implements all three methods of calculating Fibonacci numbers — recursive, iterative and Binet’s formula. Besides, a generic function for printing results of using any of the functions is defined.
package main
import ("fmt"
"math")
//Fibonacci Recursive
func fibr(n int) int {
if n < 2 { return 1 }
return fibr(n-2) + fibr(n-1)
}
//Fibonacci Iterative
func fibi(n int) int {
var a, b int = 1, 1
for i := 0; i < n; i++ {
a, b = b, a+b
}
return a
}
//Fibonacci Binet
func fibb(n int) int {
g := (1 + math.Sqrt(5)) / 2
ret := (math.Pow(g, float64(n)) - math.Pow(1-g, float64(n))) / math.Sqrt(5)
return int(ret)
}
type fibfunc func(int) int
//Implements a general printing method for fibonacci functions
func printFib(fib fibfunc, a, b int) {
for i := a; i < b; i++ {
fmt.Printf("%d, ", fib(i))
}
fmt.Println("...")
}
func main() {
printFib(fibr, 0, 16)
printFib(fibi, 0, 16)
printFib(fibb, 1, 17)
}
Example for versions Scala 2.7.7-final
This example uses recursive definition of Fibonacci numbers.
object Fibonacci {
def fibonacci(n: Int): Int =
if (n < 3) 1
else fibonacci(n - 1) + fibonacci(n - 2)
def main(args: Array[String]) {
for {i <- List.range(1, 17)}
yield { print(fibonacci(i) + ", ") }
println("...")
}
}
Example for versions Scala 2.7.7-final, Simply Scala
This example shows the usage of lazy evaluations and infinite lists in Scala. Infinite list of Fibonacci numbers is defined using functions .zip and .tail in the same way as in Haskell example.
lazy val fib: Stream[Int] = Stream.cons(1, Stream.cons(1, fib.zip(fib.tail).map(p => p._1 + p._2)))
fib.take(16).print
Example for versions gawk 3.1.6, Jawk 1.02, mawk 1.3.3
This example uses iterative definition of Fibonacci numbers. fib is an associative array, and pr is a string.
BEGIN {
fib[1] = 1
fib[2] = 1
for (i=3; i<17; i++)
fib[i] = fib[i-1]+fib[i-2]
pr = ""
for (i=1; i<17; i++)
pr = pr fib[i] ", "
print pr "..."
}
Example for versions OCaml 3.11
This example uses straightforward recursive solution. Printf.printf does formatted output.
let rec fibonacci n =
if n < 3 then
1
else
fibonacci (n-1) + fibonacci (n-2)
let () =
for n = 1 to 16 do
Printf.printf "%d, " (fibonacci n)
done;
print_endline "..."
Example for versions perl 5.8.8
This example uses recursive definition of Fibonacci numbers.
sub fibonacci {
my $n = shift;
$n < 3 ? 1 : fibonacci($n-1) + fibonacci($n-2)
}
foreach (1..16) {
print fibonacci($_), ", ";
}
print "..."
Example for versions Ruby 1.8.5
This example uses recursive definition of Fibonacci numbers.
#! /usr/bin/env ruby
def fibonacci(n)
if n < 3
1
else
fibonacci(n - 1) + fibonacci(n - 2)
end
end
(1..16).each {|n| puts fibonacci(n)}
puts "..."
Example for versions S-lang 2.2.2
This example uses iterative definition of Fibonacci numbers and shows some more features of array processing in S-lang. f is explicitly declared as an array of 16 integer numbers. Elements 0 and 1 of f are set to 1; here [0:1] creates a list of indices to which the operation is applied. Intrinsic function string converts its argument to its string representation.
f = Integer_Type [16];
f[[0:1]] = 1;
for (i=2; i<16; i++)
f[i] = f[i-1] + f[i-2];
s = "...";
for (i=15; i>=0; i--)
s = string(f[i]) + ", " + s;
message (s);
Example for versions gnuplot 4.2.2
gnuplot provides no loops, and printing each number with a separate print command makes it appear on separate line, so a string variable res is used to accumulate the calculated numbers for printing after “looping”.
### run.gp
#!/usr/bin/env gnuplot
i = 1
a = 1
b = 1
res = ''
load "fibonacci.gp"
print res, '...'
### fibonacci.gp
res = res . a . ', '
c = a
a = b
b = b+c
i = i+1
if (i <= 16) reread
Example for versions Sanscript 2.2
Sanscript is a fully visual programming language, so no source code is available. See screeshots instead.
Fibonacci numbers are calculated in the same way as factorial: a loop calculates a list of numbers, starting with two first ones, and then this list is concatenated to produce the output. Within the loop current number is added to the list and replaced with next number, while next number is replaced with a sum of current and next numbers.
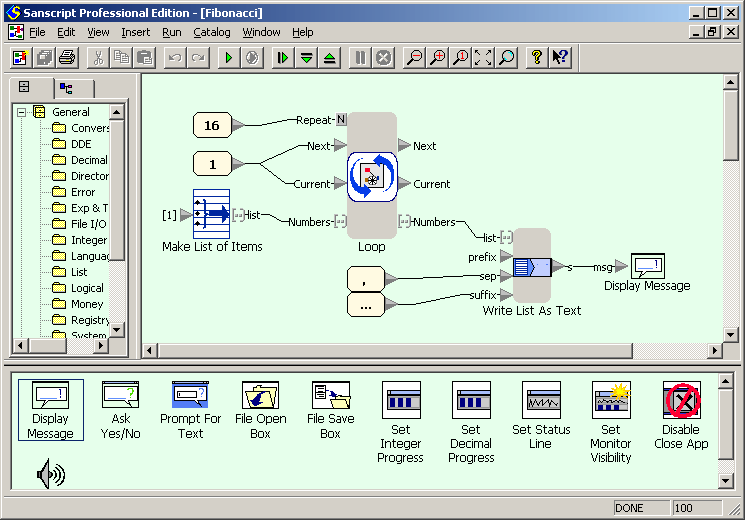
Fibonacci numbers example in Sanscript (flowgram)
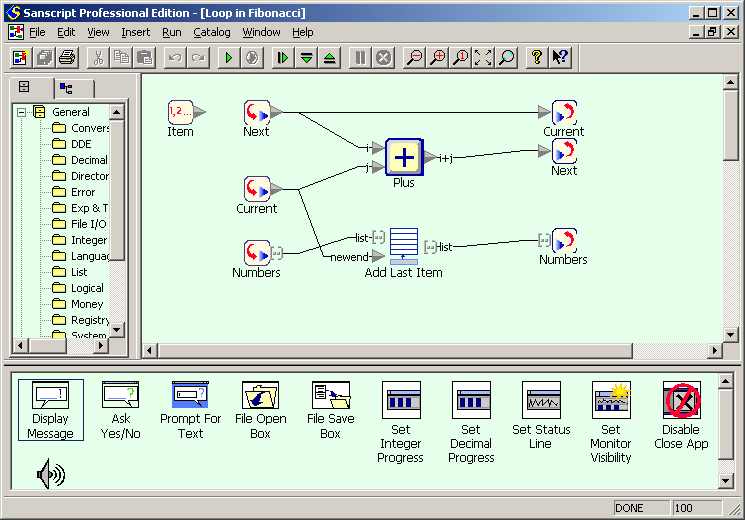
Fibonacci numbers example in Sanscript (repeat)
Example for versions Hanoi Love
This example uses iterative definition of Fibonacci numbers. Stack A is empty (used for popping 1 from it) and is used for temporary storages. Stack B holds printable characters (comma and space) and two last Fibonacci numbers. Stack C holds a 1 for each Fibonacci number to be printed (6 1’s to print 6 numbers). On each iteration one number is popped from C. If it is positive, top number f2 from stack B is popped, converted to ASCII character of the corresponding digit and printed. After this number f1 is popped from stack B and added to f2. Finally, numbers f2 and f1+f2 are pushed back in stack B. A low-level description of the example is given in the comments.
Hanoi Love interpreter uses byte variables to store values of memory cells, so a maximum of 13 Fibonacci numbers can be printed. However, printing multi-digit numbers in Hanoi Love is rather similar to Brainfuck, so only first six single-digit numbers are printed.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; .' B (space) regr = ASCII for space
...;;;;;;;;;;;;.' B (space comma) reg = ASCII for comma
..., A (empty) reg = 1
..'''''' C (6 ones for 6 numbers to print) reg = 1
..`.'...;.' B (space comma 0 1) reg = 1
., C (pop number to reg) reg = 1
.'... D (remembered this place)
: if this number is positive print top number in B and move to next Fibonacci number
..., B (space comma f1) reg = f2
.' C (f2) reg = f2
..;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; "' A (empty) reg = f2 in ASCII (printed)
., B (space comma) reg = f1
.' C (f2 f1) reg = f2
..., "' B (space) reg = comma (printed)
.' C (f2 f1 comma) reg = comma
..., "' ' B (space) reg = space (printed)
.,...' B (space comma) reg = comma
., C (f2) reg = f1
..' A (f1) reg = f1
.., C (empty) reg = f2
...' B (space comma f2) reg = f2
...; A (empty) reg = f1+f2
.' B (space comma f2 f1+f2)
., C (pop number to reg)
., D (get previous command location)
!
...,,,...;; "' "' "' pop everything from B and convert comma to point (printed three times)
Example for versions Algol68g-1.18.0, Algol68toc-1.8
Generative method. This code specimen uses a callback to generate the sequence on demand.
MODE YIELDINT = PROC(INT)VOID;
PROC fibonacci = (INT n, YIELDINT yield)VOID: (
INT even:=0, odd:=1;
yield(even);
yield(odd);
FOR i FROM odd+1 TO n DO
yield( (ODD i|odd|even) := odd + even )
OD
);
main:(
# FOR INT n IN # fibonacci(16, # ) DO ( #
## (INT n)VOID:(
print((" ",whole(n,0)))
)); # OD #
print(new line)
)
Example for versions Algol68g-1.18.0, Algol68toc-1.8
Analytic method
PROC analytic fibonacci = (INT n)INT:(
REAL sqrt 5 = sqrt(5);
REAL p = (1 + sqrt 5) / 2;
REAL q = 1/p;
ENTIER( (p**n + q**n) / sqrt 5 )
);
FOR i FROM 0 TO 16 WHILE
print(whole(analytic fibonacci(i),0));
# WHILE # i /= 16 DO
print(", ")
OD;
print(new line)
Example for versions Müller's Brainfuck 2.0
This example is a Brainloller translation of this example. Since Brainloller is a fully graphical language, no source code is available, see screenshots instead.
Fibonacci numbers example in Brainloller
Fibonacci numbers example in Brainloller (10x scale)
Example for versions Müller's Brainfuck 2.0
The program itself is too large, so it is given in shortened way. This example is a translation of Brainfuck example.
A string of
146778148267671308907956810331954494567788969820594569869966345643952713144
716974835554679004232198811425384864927587749892052914319949694507679080918
662111668706252645905597146857061868763596677983948203224834326028677131466
814323099384842068831692029352209655371798175735992788874417787727414767365
600708388513171998134124513036377960362194431944262896105838957344640161915
106378867996851411865254464299481964724009334722033995112813417289458551426
925973669722270280516592327343992579166227546099835941334220 zeros (approximately 1.5*10^509)
Example for versions Roco 20071014
This example uses iterative definition of Fibonacci numbers by saving them all in cells [2]..[17]. Cell [0] stores the index of the next number to be calculated, and cell [1] is used as temporary storage. Loops are implemented as coroutines, since by definition coroutines loop until another coroutine is called or execution is interrupted with ac command.
co calc{
/* break the loop when the counter is 2+16, since numbers start with cell 2 */
eq [1] [0] 18
if [1] ac
/* calculate next number and store it to [[0]]*/
sub [1] [0] 1
set [[0]] [[1]]
sub [1] [0] 2
add [[0]] [[0]] [[1]]
/* output */
iout [[0]]
cout 44
cout 32
/* increment counter */
add [0] [0] 1
}
/* initialize with first Fibonacci numbers */
set [0] 4
set [2] 1
set [3] 1
iout [2]
cout 44
cout 32
iout [3]
cout 44
cout 32
ca calc
cout 46
cout 46
cout 46
ac
Example for versions fsharp 2.0.0
This example uses straightforward recursive definition of Fibonacci numbers, expressed in procedural paradigm.
let rec fibonacci n =
match n with
| 1 | 2 -> 1
| _ -> fibonacci (n-1) + fibonacci (n-2)
let rec printFib n =
match n with
| 1 -> printf "%d, " (fibonacci (n))
| _ -> printFib (n-1)
printf "%d, " (fibonacci (n))
printFib(16)
printfn "..."
Example for versions Bash 4.0.35
a=0
b=1
for (( n=1; $n<=16; n=$n+1 ));
do
a=$(($a + $b))
echo -n "$a, "
b=$(($a - $b))
done
echo "..."
Example for versions Miller's Hack VM (JavaScript), Miller's Hack VM (Python)
This example works much like the other Fibonacci numbers in esoteric languages: memory cell 0 stores the number of numbers left to calculate, cells 1 and 2 store ASCII-codes for comma and space, and cells 3 and 4 store two last calculated Fibonacci numbers. In a loop values of cells 3 and 4 are extracted, added together, the new value is printed, and storage cells are updated. After this, the number of numbers left is decremented, and if it’s 0, program counter (equivalent of instruction pointer in Brainfuck) is moved 6 cell forward, otherwise it jumps back to the start of the loop. Finally, three dots are printed.
27*0> 92+4*1> 84*2> 10^p3> 1<P 2<P 10^p4> 1<P 2<P 3< 4< + 0^p 4< 3> 4> 0< 1- 0> 0< 6? 67*c 58*6+0^0^PPP
Example for versions Whitespacers (Ruby)
This example is similar to factorial one, except for that it makes more use of stack data storage and duplicate command to avoid extra readings from memory cells. Also, in this case the counter is negative and increased at each iteration, as opposed to positive and compared to fixed number of iterations.
push_1 { }
push_-16 { }
store push_2 { }
push_44 { }
store push_3 { }
push_32 { }
store push_4 { }
push_0 { }
store push_5 { }
push_1 { }
store label
{ }
start_loop_push_5 { }
push_4 { }
retrieve push_4 { }
duplicate
push_5 { }
retrieve duplicate
print_as_number
push_2 { }
retrieve print_as_char
push_3 { }
retrieve print_as_char
store retrieve add store push_1 { }
duplicate
duplicate
duplicate
retrieve add store retrieve jump_if_negative
{ }
push_10 { }
push_46 { }
duplicate
duplicate
print_as_char
print_as_char
print_as_char
print_as_char
quit
end
Example for versions erl 5.7.3
This example uses iterative definition of Fibonacci numbers, expressed as tail recursion (each number is calculated only once).
-module(prog).
-export([main/0]).
fib(1,_,Res) ->
io:format("~B, ",[Res]);
fib(N,Prev,Res) when N > 1 ->
io:format("~B, ",[Res]),
fib(N-1, Res, Res+Prev).
main() ->
fib(16,0,1),
io:format("...~n").
Example for versions erl 5.7.3
This example uses Binet’s formula to calculate Fibonacci numbers. The doubles have to be printed with at least one decimal digit, so the output looks like this:
1.0, 1.0, 2.0, 3.0, 5.0, 8.0, 13.0, 21.0, 34.0, 55.0, 89.0, 144.0, 233.0, 377.0, 610.0, 987.0, ...
-module(prog).
-export([main/0]).
fib(0) -> ok;
fib(N) ->
fib(N-1),
SQ5 = math:sqrt(5),
T1 = math:pow(0.5*(1 + SQ5),N),
T2 = math:pow(0.5*(1 - SQ5),N),
io:format("~.1f, ", [(T1-T2)/SQ5]).
main() ->
fib(16),
io:format("...~n").
Example for versions j602
Maxtrix closed form
load 'printf'
mat =: 1 1,.1 0
fibm=: 3 : '1 { , mat&(+/ . *)^:y mat'"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibm >:i.16
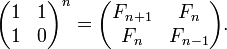
Fibonacci Matrix Closed Form
Example for versions B-Prolog 7.4 #3, gprolog 1.3.0, swipl 5.6.x
Once again, the example is almost identical to Poplog Prolog one, except for the syntax of compiling/consulting a file.
% fibonacci.pl
:- dynamic(stored/1).
memo(Goal) :-
stored(Goal) -> true;
Goal, assertz(stored(Goal)).
fib(1,1) :- !, write('1, ').
fib(2,1) :- !, write('1, ').
fib(N,F) :-
N1 is N-1, memo(fib(N1,F1)),
N2 is N-2, memo(fib(N2,F2)),
F is F1 + F2,
write(F), write(', ').
% interactive
[fibonacci].
fib(16,X), write('...'), nl.
Example for versions bc 1.06
This example uses recursive definition of Fibonacci numbers. Note that printing “…” is put into the loop, since both code and output are shown in the same console, and printing “…” after the loop will result in the following output:
for (n = 1; n <= 16; n++) {
print fibonacci(n); ", "
}
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, print "..."
...
define fibonacci(n) {
if (n <= 2) return(1);
return(fibonacci(n-1)+fibonacci(n-2));
}
for (n = 1; n <= 16; n++) {
print fibonacci(n); ", "
if (n==16) print "..."
}
Example for versions bc 1.06
This example uses Binet’s formula. Note that bc is an arbitrary-precision calculator, so after floating-point calculations the numbers have to be rounded to integers. This has to be done manually, since bc doesn’t provide built-in rounding.
for (n = 1; n <= 16; n++) {
scale = 10
x = (((1 + sqrt(5)) * .5) ^ n - ((1 - sqrt(5)) * .5) ^ n) / sqrt(5)
scale = 0
print (x+0.5)/1; ", "
if (n==16) print "..."
}
Example for versions boo 0.8.2
This example uses iterative definition of Fibonacci numbers. The array a is declared to have 16 elements right away, and the elements are calculated later.
a = array(int, 16)
a[0] = a[1] = 1
for i in range(2,16):
a[i] = a[i-1] + a[i-2]
s=""
for i in range(16):
s = s + a[i] + ", "
print(s + "...")
Example for versions boo 0.8.2
This example shows the usage of generator fib: it initializes inner variables a and b, and after each call to generator it updates the variables and returns one of them. Function zip is a built-in which returns an IEnumerable that is a “mesh” of two IEnumerables — range and fib.
def fib():
a, b = 0, 1
while true:
yield b
a, b = b, a + b
s=""
for i, n in zip(range(16), fib()):
s = s+n+", "
print(s+"...")
Example for versions gforth 0.7.0
This example uses iterative definition of Fibonacci numbers.
: fib-iter
0 1 rot 0 ?do over + swap loop drop ;
: lp
1 do
i dup fib-iter . ." , "
loop drop ;
17 lp
." ..."
Example for versions gforth 0.7.0
This example uses recursive definition of Fibonacci numbers.
: fib-rec
dup 2 u< if exit then
1- dup recurse swap 1- recurse + ;
: lp
1 do
i dup fib-rec . ." , "
loop drop ;
17 lp
." ..."
Example for versions c-intercal 28.0, J-INTERCAL 0.11, J-INTERCAL 0.12
This example uses iterative definition of Fibonacci numbers. Variables .10 and .11 store previous and current calculated numbers, and .9 stores the number of iterations left.
Loop body is quite simple: print current number .11, copy .10 and .11 to .1 and .2, add them ((1009) NEXT calls addition from standard library and puts sum to .3) and update the values. The trickiest part of the program is the code that implements looping behavior. Here is what it does.
(3) NEXT and (4) NEXT move execution to label (4). At this line the loop counter .9 is updated by subtracting 1 from it (call of (1010)). After this, .1 is calculated in a rather complicated way that makes it 1 if .9 is non-zero, and 0 otherwise. After this, .1 is incremented to be 1 if the loop has to stop (loop counter is zero) and 2 otherwise. Finally, RESUME .1 is performed to return to one of the NEXTs applied. If .1 is 2, the program returns two NEXTs back, and continues with DO (1) NEXT which brings it to the start of the loop again. However, if .1 is 1, the program returns one NEXT back, continues with PLEASE GIVE UP and halts.
Note that numbers are printed in Roman notation (this language lets not a single thing be easy!), one number per two lines (line which is empty in this example is for modifiers), so the output looks like this:
I
I
II
III
V
VIII
XIII
XXI
XXXIV
LV
LXXXIX
CXLIV
CCXXXIII
CCCLXXVII
DCX
CMLXXXVII
DO .9 <- #16
DO .10 <- #0
DO .11 <- #1
(1) PLEASE READ OUT .11
DO .1 <- .10
DO .2 <- .11
PLEASE (1009) NEXT
DO .10 <- .11
DO .11 <- .3
DO (3) NEXT
DO (1) NEXT
(3) DO (4) NEXT
PLEASE GIVE UP
(4) DO .1 <- .9
DO .2 <- #1
PLEASE (1010) NEXT
DO .9 <- .3
DO .1 <- '.9~.9'~#1
PLEASE (1020) NEXT
DO RESUME .1
Example for versions Mozart 1.4.0
This example uses iterative definition of Fibonacci numbers.
functor
import
Application System
define
local
A B C S
in
A = {NewCell 0}
B = {NewCell 1}
C = {NewCell 0}
S = {NewCell ""}
for I in 1..16 do
C := @A + @B
A := @B
B := @C
S := {Append {Append @S {Int.toString @A}} ", "}
end
{System.showInfo {Append @S "..."}}
{Application.exit 0}
end
end
Example for versions Mozart 1.4.0
This example uses tail-recursive definition of Fibonacci numbers.
functor
import
Application System
define
fun{Fib N}
fun{Loop N A B}
if N == 0 then
B
else
{Loop N-1 A+B A}
end
end
in
{Loop N 1 0}
end
local
S
in
S = {NewCell ""}
for I in 1..16 do
S := {Append {Append @S {Int.toString {Fib I}}} ", "}
end
{System.showInfo {Append @S "..."}}
{Application.exit 0}
end
end
Example for versions gst 3.1
This example uses iterative definition of Fibonacci numbers,.
a1 := 0.
a2 := 1.
0 to: 15 do: [ :i |
a2 display.
t := a1 + a2.
a1 := a2.
a2 := t.
', ' display
]
'...' displayNl.
Example for versions ActiveTcl 8.5, Tcl 8.5.7
This example uses iterative definition of Fibonacci numbers. lassign assigns successive elements from the list passed as first argument (created by [list ...]) to the variables given by the next arguments (fib1 and fib2 in this case). This command was moved to language core in Tcl 8.5; before that it was part of TclX package.
set fib1 0
set fib2 1
set s ""
for {set i 0} {$i < 16} {incr i} {
lassign [list $fib2 [incr fib2 $fib1]] fib1 fib2
append s "$fib1, "
}
puts "$s..."
Example for versions GHC 6.10.4
This is another example which uses lazy evaluation and a different, shorter form of producing output in required format.
main = putStrLn $ withDots $ join $ take 16 fibs
where fibs = 1 : 1 : zipWith (+) fibs (tail fibs)
join = foldl (\a b -> a ++ show b ++ ", " ) ""
withDots = (++ "...")
Example for versions ActiveTcl 8.5, Tcl 8.5.7
This example uses recursive definition of Fibonacci numbers. Function fib is defined in namespace tcl::mathfunc, so that it can be used as math function in expr expressions.
proc tcl::mathfunc::fib {n} {
if {$n<=1} {
return 1
} else {
return [expr fib([expr {$n - 1}]) + fib([expr {$n - 2}])]
}
}
set s ""
for {set i 0} {$i < 16} {incr i} {
append s [expr fib($i)] ", "
}
puts "$s..."
Example for versions ncc 0.9.3
This example uses recursive definition of Fibonacci numbers, expressed in functional style. Note the definition of loop counter i — keyword mutable, as opposed to regular def, means that the value of the variable is going to change.
def fib(i)
{
| x when x<2 => 1
| _ => fib(i - 2) + fib(i - 1)
}
mutable i=0;
while (i<16)
{ System.Console.Write("{0}, ", fib(i));
i++;
}
System.Console.WriteLine("...");
Example for versions Web2c 2009
This example uses iterative process to calculate Fibonacci numbers.
Note that \fibonacci macro has to use double curly brackets because it has loop that is used inside other loop.
\newcount\n \newcount\np \newcount\npp \newcount\m \newcount\f
\def\fibonacci#1{{\ifnum #1<3 1\else
\np=1\npp=1\m=3
\loop\ifnum\m<#1\f=\npp\npp=\np\advance\np by\f\advance\m by 1\repeat
\f=0\advance\f by\np\advance\f by\npp
\number\f\fi}}
\def\printfibonacci#1{\m=#1\advance\m by 1
\n=1
\loop\ifnum\n<\m\fibonacci{\n}, \advance\n by 1\repeat...}
\printfibonacci{16}
\bye
Example for versions Baltie 3
The example is rather self-explanatory: boxes A..D are global variables (blue for integer, yellow for string). Arrow facing left is assignment. For loop takes variable, range start and range end as parameters in round brackets, loop body is enclosed in {} brackets.
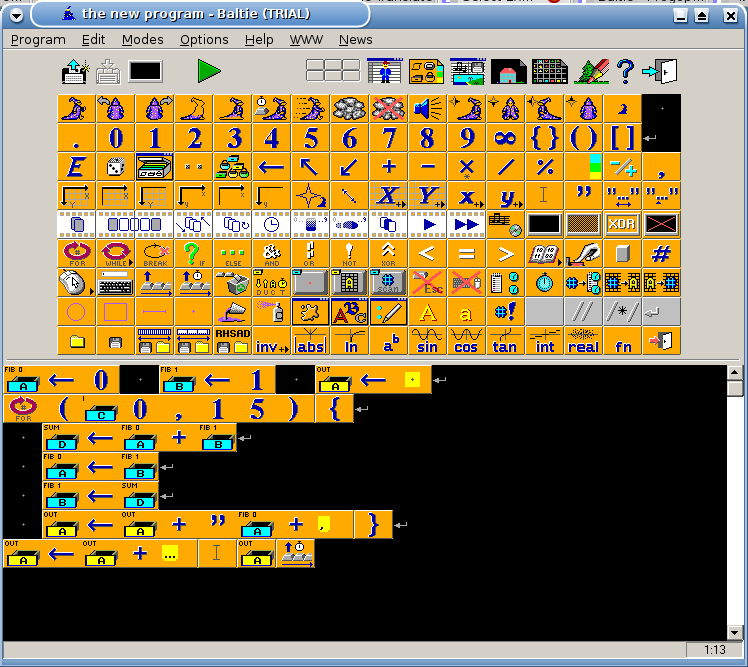
Fibonacci numbers in Baltie 3
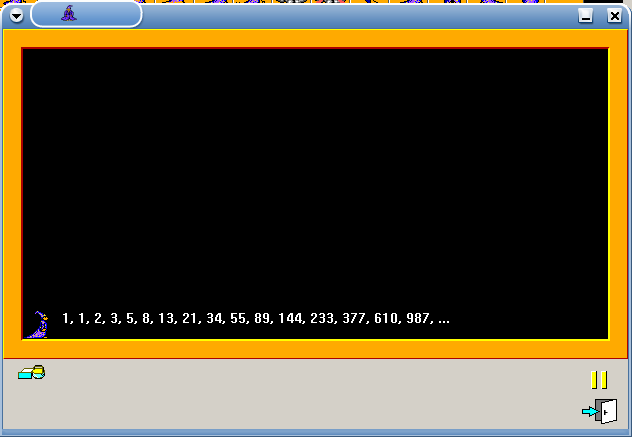
Fibonacci numbers in Baltie 3 (result)
Example for versions Io-2008-01-07
This example uses iterative definition of Fibonacci numbers. for loop misses fourth parameter which sets loop step — it defaults to 1, so no need to set it explicitly.
N0 := 0;
N1 := 1;
for(i,1,16,
N2 := N1+N0;
N0 := N1;
N1 := N2;
N0 print;
", " print;
);
"..." println;
Example for versions Io-2008-01-07
This example uses Binet’s formula. Math functions are called by sending a message to the number which is an object as well.
g := (5 sqrt + 1) / 2;
for(i,1,16,
N := ((g pow(i)) - ((1-g) pow(i))) / (5 sqrt);
N round print;
", " print;
);
"..." println;
Example for versions Online Cat 1.3
This example uses recursive definition of Fibonacci numbers. First part defines a function fib which works as follows. When it is called, the top element of the stack is index of Fibonacci number to be calculated. First the commands dup and 1 push a copy of this element and a 1 on the stack. Then command <= (which is equivalent of lteq) pops and compares top two elements and pushes true if index is less than or equal to 1, and false otherwise.
Next goes conditional expression: two quotations are pushed on the stack, and then if the third-top element of the stack is true, first of them is evaluated, otherwise second one is. In this case true-quotation is empty (Fibonacci numbers 0 and 1 are equal to 0 and 1, respectively, so no calculations are required), and false-quotation is the following. It duplicates the top element of the stack (which is index N of the number again), decrements the duplicated value (N-1), calculates Fibonacci number N-1 and replaces the index with the number itself, swaps two top elements of the stack (so now they are Fib(N-1) N), subtracts 2 from the top element (N-2) and replaces it with respective Fibonacci number. Finally, two Fibonacci numbers are added to get the number which was required.
Second part of the program is its body which loops over the indices from 1 to 16, calculates numbers and prints them. It uses a while-loop, with body [dup fib write ", " write inc] which duplicates top element of the stack, calculates its Fibonacci number, writes it, writes comma after it and increments the loop counter. [dup 16 lteq] is condition of repeating the loop — while loop counter is less than or equal to 16.
define fib {
dup 1 <=
[]
[dup 1 - fib swap 2 - fib +]
if
}
1
[dup fib write ", " write inc]
[dup 16 lteq]
while
"..." writeln
Example for versions 64-bit BCPL Cintcode System (1 Nov 2006)
This example uses recursive definition of Fibonacci numbers.
GET "libhdr"
LET start() = VALOF
{ FOR i = 0 TO 15 DO writef("%n, ", fibonacci(i))
writef("...*n")
RESULTIS 0
}
AND fibonacci(n) = n<2 -> 1, fibonacci(n-1)+fibonacci(n-2)
Example for versions Acme-Chef-1.01
This example uses iterative calculation of Fibonacci numbers. Last and one-before-last calculated numbers are stored in ingredients fib1 and fib2, respectively. In one iteration of loop chop ... until choped the next number is calculated, and the previous one is written to the stack for being printed later. Second loop mash ... until mashed pours the values from first bowl into second one, so that they can be printed in correct (increasing) order.
This version of the interpreter doesn’t allow to hold liquid and dry ingredients on one stack, and thus disallows printing both numbers and characters in one message. This punctuation has been dropped from the output; the result looks as follows:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
Fibonacci numbers.
This recipe calculates and prints first Fibonacci numbers.
Ingredients.
0 g fib1
1 g fib2
16 g iterator
16 g second iterator
Method.
Chop iterator.
Put fib2 into 1st mixing bowl.
Put fib2 into 1st mixing bowl.
Add fib1 into 1st mixing bowl.
Fold fib2 into 1st mixing bowl.
Fold fib1 into 1st mixing bowl.
Put fib1 into 1st mixing bowl.
Chop iterator until choped.
Mash second iterator.
Fold fib1 into 1st mixing bowl.
Put fib1 into 2nd mixing bowl.
Mash second iterator until mashed.
Pour contents of 2nd mixing bowl into the baking dish.
Serves 1.
Example for versions OpenCOBOL 1.0, TinyCOBOL 0.65.9
This example uses iterative calculation of Fibonacci numbers. Two numbers are added using command ADD which puts the sum of two arguments in the third one. DISPLAY adds a newline after each item it prints, so all numbers have to be concatenated in one string before being printed. To do this, STRING command is used. For each item concatenated one has to set DELIMITED BY option: SIZE — all variable is used (declared size of it), SPACE — the part of the variable till first whitespace. This means that the concatenated string can’t contain spaces, and the output looks like this:
001,001,002,003,005,008,013,021,034,055,089,144,233,377,610,987,...
IDENTIFICATION DIVISION.
PROGRAM-ID. SAMPLE.
DATA DIVISION.
WORKING-STORAGE SECTION.
77 fib1 pic 999.
77 fib2 pic 999.
77 fib3 pic 999.
77 i pic 99.
77 fibst pic XXX.
77 res pic X(64).
PROCEDURE DIVISION.
move 0 to i
move 0 to fib1
move 1 to fib2
move "" to res
perform until i greater than 15
add fib1 to fib2 giving fib3
move fib2 to fib1
move fib3 to fib2
move fib1 to fibst
string res DELIMITED BY SPACE
fibst DELIMITED BY SIZE
"," DELIMITED BY SIZE into res
add 1 to i
end-perform.
display res "..."
stop run.
Example for versions Pike 7.8
This example uses recursive definition of Fibonacci numbers.
int fibonacci(int n)
{
return ( n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2) );
}
void main()
{
for (int n=1; n<=16; n++)
write(fibonacci(n)+", ");
write("...\n");
}
Example for versions befungee 0.2.0
This example uses iterative definition of Fibonacci numbers. It is based on commands p and g which are used to modify source code of the program at the runtime, — they put a specific character at a certain cell of the program or read it from the cell to the stack, respectively. In this case they are used to store Fibonacci numbers outside of the stack. Loop counter is stored in the bottom element of the stack all the time. Since playfield cells can’t store values over 255, only the first 13 Fibonacci numbers are printed.
031p132p 94+ > 31g 32g :. + 32g v
| :-1,,", "p23 p13 <
> "."::,,,@
Example for versions Objeck 2.0.3
This example uses recursive definition of Fibonacci numbers.
bundle Default {
class Fib {
function : Fibonacci (n: Int) ~ Int {
if (n<=2) {
return 1;
};
return Fibonacci(n-1) + Fibonacci(n-2);
}
function : Main(args : String[]) ~ Nil {
for (i := 0; i <= 16; i += 1;) {
Fibonacci(i)->Print();
", "->Print();
};
"..."->PrintLine();
}
}
}
Example for versions Morphett's FALSE, Wouter's FALSE 1.2.CF
This example uses iterative method of calculating Fibonacci numbers. Variables a and b store current numbers, variable i is loop counter.
The second loop empties the stack (deletes Fibonacci numbers written there by the first loop). Some interpreters tolerate data left in stack after program completion, but Wouter’s FALSE requires that the stack is empty and throws a runtime error otherwise.
0i: 1a: 1b:
[i;16=~]
[a; $. ", " $ b; $ a: + b: i;1+i:]
#
"..."
[1=~]
[]
#
%
Example for versions Lingua::Shakespeare 1.00
This example uses iterative method of calculating Fibonacci numbers. After the loop (end of scene II) loop counter Isabella is re-used to print full stops.
use Lingua::Shakespeare;
Fibonacci Numbers.
Isabella, the loop index.
Falstaff, a Fibonacci number.
Fortinbras, another Fibonacci number.
Sebastian, space.
Cordelia, comma.
Act I: Factorial calculations.
Scene I: Initialization.
[Enter Isabella and Sebastian]
Isabella:
You are as fat as the product of a big black furry old cat and a white cow!
[Exit Sebastian]
[Enter Cordelia]
Isabella:
You are as beautiful as the sum of Sebastian and the sum of a tiny yellow furry hamster and the clearest blue sky!
[Exit Cordelia]
[Enter Fortinbras]
Isabella:
You father!
Scene II: Loop.
Isabella:
Open your heart!
You are as noble as the sum of yourself and Falstaff.
[Exit Fortinbras]
[Enter Falstaff]
Isabella:
You are as brave as the difference between Fortinbras and yourself.
[Exit Falstaff]
[Enter Cordelia]
Isabella:
Speak your mind!
[Exit Cordelia]
[Enter Sebastian]
Isabella:
Speak your mind!
[Exit Sebastian]
[Enter Fortinbras]
Fortinbras:
You are as good as the sum of yourself and a rose.
Isabella:
Am I not as beautiful as your sweet charming lovely noble sister?
Fortinbras:
If so, let us return to scene II.
You are as good as the sum of Cordelia and a fine horse!
Speak your mind! Speak your mind! Speak your mind!
[Exeunt]
Example for versions SML/NJ 110
This example uses straightforward recursive solution. The print function prints strings. The ^ operator concatenates strings. The Int.toString function converts integers into strings.
fun fibonacci n =
if n < 3 then
1
else
fibonacci (n-1) + fibonacci (n-2)
fun aux n =
if n > 16 then
print "\n"
else (
print (Int.toString (fibonacci n) ^ ", ");
aux (n + 1)
);
aux 1;
Example for versions npiet 1.2
This example was generated automatically. The original program translated into the image follows; it uses iterative calculation of Fibonacci numbers.
main()
{
f1 = 0;
f2 = 1;
for ( i = 1; i <= 16; i++ )
{
__outn(f2);
__out(44);
__out(32);
f2 = f1 + f2;
f1 = f2 - f1;
}
__out(46);
__out(46);
__out(46);
__out(10);
}

Fibonacci numbers in Piet (autogenerated)
Fibonacci numbers in Piet (autogenerated, 4x scale)
Example for versions GNU Octave 3.2.3
This example uses recursive definition of Fibonacci numbers.
function f = fib(n)
if (n <= 1)
f = n;
else
f = fib(n - 1) + fib(n - 2);
endif
endfunction
for i = 1 : 16
printf("%d, ", fib(i));
endfor
disp("...");
Example for versions ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
This example uses iterative definition of Fibonacci numbers.
set fib1 0
set fib2 1
set s ""
for {set i 0} {$i < 16} {incr i} {
set fib3 [expr {$fib1 + $fib2}]
set fib1 $fib2
set fib2 $fib3
append s "$fib1, "
}
puts "$s..."
Example for versions ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
This example uses tail recursion to calculate the numbers. eval command allows to evaluate the result of calling fib with given arguments without declaring fib as part of any namespace.
proc fib {f1 f2 n} {
if {$n==0} {
return $f1
} else {
return [eval fib $f2 [expr {$f1 + $f2}] [expr {$n - 1}]]
}
}
set s ""
for {set i 0} {$i < 16} {incr i} {
append s [eval fib 1 1 $i] ", "
}
puts "$s..."
Example for versions guile 1.8.5, JScheme 7.2, MIT/GNU Scheme 7.7.9
This example uses recursive definition of Fibonacci numbers.
(define (fibonacci x)
(if (< x 2)
x
(+ (fibonacci (- x 1)) (fibonacci (- x 2)))))
(do ((i 1 (+ i 1)))
((> i 16))
(display (string-append (number->string (fibonacci i)) ", ")))
(display "...")
(newline)
Example for versions Clojure 1.0.0, Clojure 1.1.0
This example uses recursive definition of Fibonacci numbers.
(defn fibonacci [x]
(if (< x 2)
x
(+ (fibonacci (- x 1)) (fibonacci (- x 2)) )))
(doseq [i (range 1 17)]
(print (str (fibonacci i) ", ")))
(println "...")
Example for versions Seed7 2012-01-01
This example uses recursive definition of Fibonacci numbers.
$ include "seed7_05.s7i";
const func integer: fibonacci (in var integer: n) is func
result
var integer: result is 1;
begin
if n < 2 then
result := 1;
else
result := fibonacci(n - 1) + fibonacci(n - 2);
end if;
end func;
const proc: main is func
local
var integer: n is 0;
begin
for n range 0 to 15 do
write(fibonacci(n) <& ", ");
end for;
writeln("...");
end func;
Example for versions Falcon 0.9.6.6
This example uses recursive definition of Fibonacci numbers.
function fib(n)
if n <= 2 : return 1
return fib(n-1) + fib(n-2)
end
for i in [1:17]
print (fib(i), ", ")
end
printl ("...")
Example for versions iconc 9.4
This example uses recursive calculation of Fibonacci numbers with memoization.
global fib_memo
procedure fib (n)
if n >= 0 then
return ((/fib_memo [n] := fib (n - 2) + fib (n - 1)) | fib_memo [n])
end
procedure main ()
local i
fib_memo := table ()
fib_memo [0] := 0; fib_memo [1] := 1
every i := 1 to 16 do {
writes (fib (i) || ", ")
}
write("...")
end
Example for versions Rust 0.1
This example calculates Fibonacci numbers recursively.
use std;
import std::io;
fn fibonacci(x: int) -> int {
if (x <= 2) {
ret 1;
} else {
ret fibonacci(x - 1) + fibonacci(x - 2);
}
}
fn main() {
let i = 1;
while i <= 16 {
io::print(#fmt("%d, ", fibonacci(i)));
i = i + 1;
}
io::println("...");
}
Example for versions Ceylon M1
This example calculates Fibonacci numbers iteratively.
void run() {
variable String output := "";
variable Integer fib1 := 0;
variable Integer fib2 := 1;
variable Integer fib3;
for (i in 1..16) {
output := "" output "" fib2 ", ";
fib3 := fib1 + fib2;
fib1 := fib2;
fib2 := fib3;
}
print("" output "...");
}
Example for versions Factor 0.94
This example shows recursive calculation of Fibonacci numbers.
Word fib calculates the n-th number: if the argument is not greater than 1, it stays on the stack as the return value, otherwise it is replaced with a sum of previous numbers. Word bi is a short-hand version of cleave combinator and allows to apply two quotations (in this case calls of fib for smaller arguments) to the same element of the stack (n).
USING: formatting kernel math sequences ;
IN: fibonacci-example
: fib ( n -- fib(n) )
dup
1 >
[ [ 1 - fib ] [ 2 - fib ] bi + ]
when ;
16 iota [ 1 + fib "%d, " printf ] each
"...\n" printf
Example for versions loljs 1.1
HAI
I HAS A I ITS 0
I HAS A FIB1 ITS 0
I HAS A FIB2 ITS 1
IM IN YR LOOP UPPIN YR I TIL BOTH SAEM I AN 16
VISIBLE SMOOSH FIB2 ", "!
I HAS A FIB3 ITS SUM OF FIB1 AN FIB2
FIB1 R FIB2
FIB2 R FIB3
IM OUTTA YR LOOP
VISIBLE "..."
KTHXBYE
Example for versions loljs 1.1
HAI
HOW DUZ I FIBONACCI N
BOTH SAEM 1 AN BIGGR OF N AN 1, O RLY?
YA RLY
FOUND YR 1
NO WAI
FOUND YR SUM OF FIBONACCI DIFF OF N AN 1 AN FIBONACCI DIFF OF N AN 2
OIC
IF U SAY SO
I HAS A N ITZ 0
IM IN YR LOOP UPPIN YR N WILE N SMALLR THAN 16
VISIBLE SMOOSH FIBONACCI N ", "!
IM OUTTA YR LOOP
VISIBLE "..."
KTHXBYE
Example for versions Mathics 0.5, Wolfram Mathematica 8.0.4
Print always outputs a newline after the output, so to prints the numbers in a single line, one has to accumulate them into a string and print it. <> is concatenation operator, it works only on strings, so the result of Fibonacci call must be converted to string explicitly using ToString function.
msg = "";
Do[msg = msg <> ToString[Fibonacci[i]] <> ", " , {i, 16} ];
Print[msg, "..."];
Example for versions PostgreSQL 9.1
WITH RECURSIVE t(a,b) AS (
VALUES(1,1)
UNION ALL
SELECT b, a + b FROM t
WHERE b < 1000
)
SELECT array_to_string(array(SELECT a FROM t), ', ') || ', ...';
Example for versions Dyalog APL 13.1
This example uses Binet’s formula implemented via an anonymous D-function. ⋄ is expression separator, so the function consists of two expressions evaluated in left-to-right order. The first one calculates golden ration and binds it to name phi. The second one calculates the value of the function (Fibonacci number) based on its right argument ⍵ (the index of the number). ⌈ rounds the number up.
Since the function is unary and is defined using scalar functions only, it can be applied to an array — in this case to an array of indices between 1 and 16, inclusive. This will result in an array of Fibonacci numbers:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
{phi←(1+5*0.5)÷2 ⋄ ⌈((phi*⍵) - (1-phi)*⍵)÷5*0.5} 1+⍳16
Example for versions Dyalog APL 13.1
This example uses an anonymous D-function which calls itself recursively. The first expression of the function processes the case of the first two Fibonacci numbers, returning 1. The rest of them are processed by the second expression, which calls this very D-function (function ∇) for smaller indices of the numbers and sums them. Overall the first line of code associates the calculated array of numbers with name fib and outputs nothing.
The second line converts the array to required format: each element gets concatenated with a comma separator, all elements of the resulting array get concatenated with each other (,/), and the result is padded with .... The overall output of this line looks exactly as required:
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 , 610 , 987 , ...
fib←{⍵≤2:1 ⋄ (∇⍵-1)+∇⍵-2}¨1+⍳16
(⊃(,/{⍵, ', '}¨fib)),'...'
Example for versions Nimrod 0.8.8
This example uses iterative calculation of Fibonacci numbers. A single var keyword can declare several variables if they are indented to form a block. Note that variable type can be omitted from the declaration only if it is initialized immediately; Nimrod uses local type inference, not global one.
for i in 1..16 is an alternate form of writing countup loop. & is string concatenation operator, and $ is number-to-string conversion.
var
f1 = 1
f2 = 1
f3: int
res = ""
for i in 1..16:
res = res & $f1 & ", "
f3 = f1 + f2
f1 = f2
f2 = f3
echo res & "..."
Example for versions Nimrod 0.8.8
This example uses Binet’s formula to calculate the numbers. Addition of epsilon value before rounding is necessary to get exact integer values.
from math import sqrt, pow, round
proc fibonacci(n: int): int =
var phi: float64 = (1.0 + sqrt(5.0)) / 2.0
return round((pow(phi, float64(n)) - pow(-phi, -float64(n))) / sqrt(5.0) + 0.0001)
var res = ""
for i in 1..16:
res = res & $fibonacci(i) & ", "
echo res & "..."
Example for versions bwBASIC 2.50
This example shows iterative calculation of Fibonacci numbers and storing them in an array. Note the explicit array declaration and the string variable S$ — string variables names must end with a $.
DIM F(16)
F(1) = 1
F(2) = 1
FOR i = 3 TO 16
F(i) = F(i - 1) + F(i - 2)
NEXT i
S$ = ""
FOR i = 1 TO 16
S$ = S$ + STR$(F(i)) + ","
NEXT i
S$ = S$ + " ..."
PRINT S$
Example for versions VBScript 5.7, VBScript 5.8
This program calculates Fibonacci numbers recursively. Note the absence of a lot of elements typical for other Basic dialects: variable declarations and function return type, explicit number-to-string conversion before concatenation etc.
Function Fibonacci(N)
If N < 2 Then
Fibonacci = N
Else
Fibonacci = Fibonacci(N - 1) + Fibonacci(N - 2)
End If
End Function
For i = 1 To 16
res = res & Fibonacci(i) & ", "
Next
WScript.Echo (res & "...")
Example for versions A++ Interpreter
This example uses tail recursion.
(load "app/init.app")
(define fibonacci (lambda(f1 f2 n)
(if (equal n 0)
f1
(fibonacci f2 (+ f1 f2) (- n 1)))
))
(define main
(lambda(n)
(while (not (equal n 16))
(lambda()
(print (fibonacci 1 1 n))
(define n (+ n 1))))))
(main 0)
Example for versions E-on-Java 0.9.3
var s := [0, 1]
var res := ""
for _ in 1..16 {
def [a, b] := s
s := [b, a + b]
res := res + b.toString(10) + ", "
}
println(res + "...")
Example for versions Mathics 0.5
This example uses Riffle function which in this case alternates elements of the array containing Fibonacci numbers and the separator string “,”.
StringJoin[Riffle[Map[ToString, Table[Fibonacci[i], {i,16}]], ", "]] <> "..."
Example for versions Dart 1.1.1
This example uses recursive definition of Fibonacci numbers. Note that the language requires explicit conversion from int to String.
int fibonacci(int n) => n <= 2 ? 1 : fibonacci(n - 2) + fibonacci (n - 1);
main() {
String output = "";
for (int i = 1; i <= 16; ++i) {
output += fibonacci(i).toString() + ", ";
}
print(output + "...");
}
Example for versions Snap! 4.0
This example uses recursive calculation of Fibonacci numbers. To speed up calculations, newly found numbers are written to “cache” which is simply a global list.
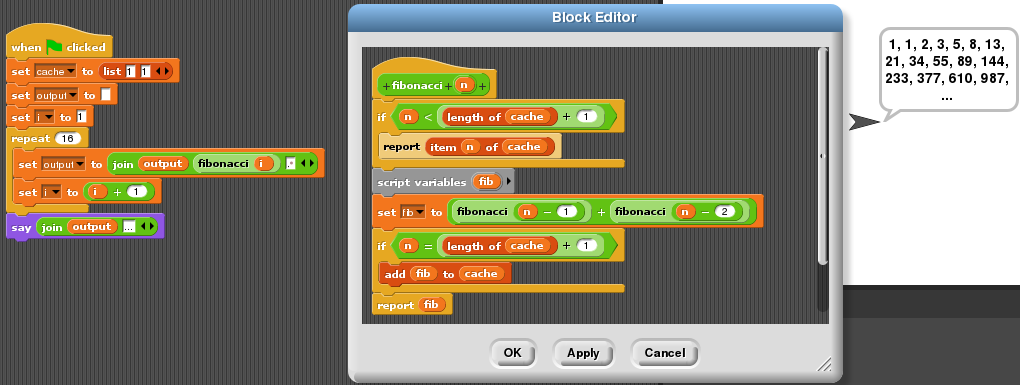
Fibonacci numbers (recursive) in Snap!
Example for versions Windows PowerShell 5.0
function Get-Fibonacci ($n) {
if ($n -le 1) {
return 1
}
return (Get-Fibonacci ($n - 1)) + (Get-Fibonacci ($n - 2))
}
$output = ""
foreach ($i in 0..15) {
$output += ("{0}, " -f (Get-Fibonacci $i))
}
echo "$output..."
Example for versions W 1.1.0
REF "Runtime.IO"
Item x = 1
Item y = 1
Type(x)
Repeat 15
[
Type(y)
Item z = x + y
x = y
y = z
]