Algol68g-1.18.0
Version of implementation Genie Algol68g of programming language Algol68What is new in Algol 68 Genie Version 1.18.0?
- Regression fixes: · Rowing failed for some flexible rows, · Generator failed for some structures, · Garbage collector could crash under rare circumstances, · Some flexible mode declarations were not accepted, · Some modes were incorrectly marked as equivalent, · Unnecessary size limitations in some matrix operations, · Build error on MacOS X, · Alignment error on AMD64.
- Adds NEW as alternative to HEAP.
- More efficient use of memory during compilation.
- Documentation updates.
- Upon request, re-post the HTML translation of the Revised Report.
- Change to a common Linux-style version numbering (former Mark j will now read Version 1.j.0, and former Mark j.k will now read Version 1.j.k).
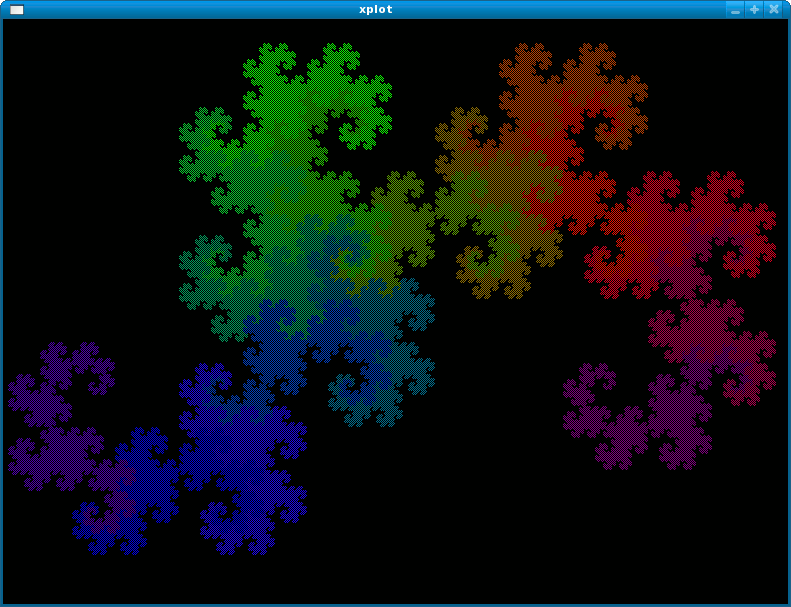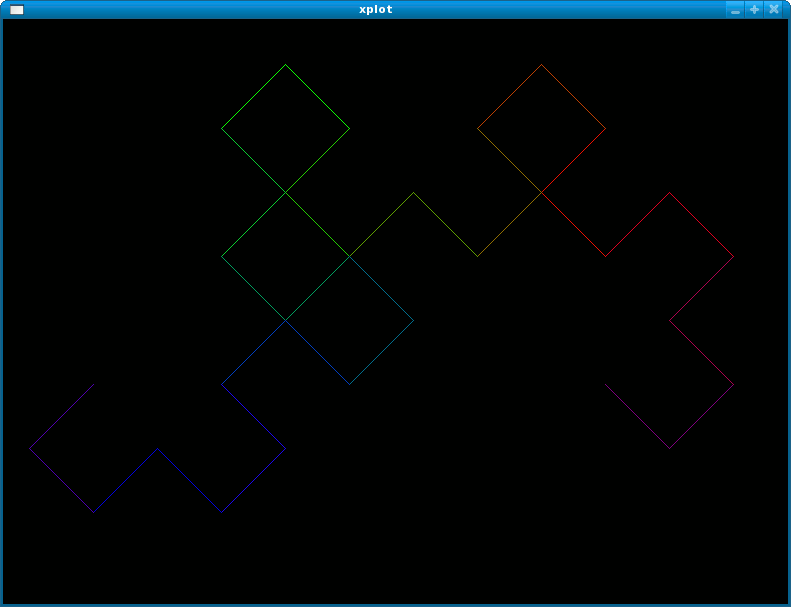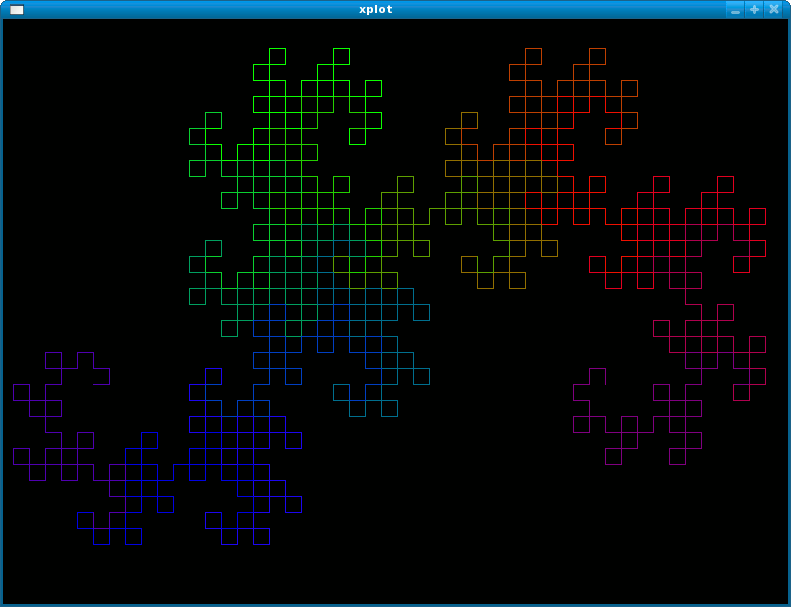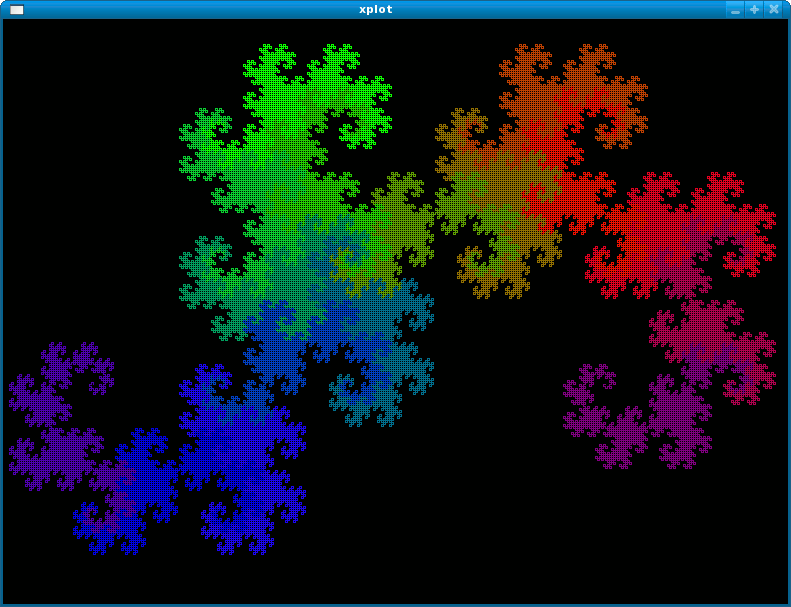
ALGOL 68 Dragon curve animated
Links:
Examples:
Hello, World! - Algol68 (107):
Note the use of printf with the formatting being described between dollars. eg $gl$ — meaning “g”eneral pattern, then new “l”ine.
(
printf(($gl$,"Hello, world!"))
)
Factorial - Algol68 (108):
This example uses recursive factorial definition with first 7 numbers precomputed.
PROC factorial = (INT n)LONG LONG INT:
CASE n+1 IN
1,1,2,6,24,120,720 # a brief lookup #
OUT
n*factorial(n-1)
ESAC
;
Quadratic equation - Algol68 (163):
A direct translation of the C++ example.
PROC print root = (INT ind, LONG COMPL x)VOID:
( print(("x", ind, " := "));
IF ABS(im OF x) < 1E-6 THEN
print((re OF x, new line))
ELSE print((x, new line))
FI
);
main:
( LONG COMPL a, b, c, d, x1, x2;
print(("a := "));
read((a));
IF ABS a <1E-3 THEN
print(( "Not a quadratic equation", new line));
stop
FI;
print(("b := "));
read((b));
print(("c := "));
read((c));
a *:= 2;
d := b*b-a*c*2.0;
IF ABS d <1E-3 THEN
print(("x := ", re OF (-b/a)))
ELSE
print root(1, (-b+long complex sqrt(d))/a);
print root(2, (-b-long complex sqrt(d))/a)
FI
)
Fibonacci numbers - Algol68 (187):
Generative method. This code specimen uses a callback to generate the sequence on demand.
MODE YIELDINT = PROC(INT)VOID;
PROC fibonacci = (INT n, YIELDINT yield)VOID: (
INT even:=0, odd:=1;
yield(even);
yield(odd);
FOR i FROM odd+1 TO n DO
yield( (ODD i|odd|even) := odd + even )
OD
);
main:(
# FOR INT n IN # fibonacci(16, # ) DO ( #
## (INT n)VOID:(
print((" ",whole(n,0)))
)); # OD #
print(new line)
)
Fibonacci numbers - Algol68 (188):
Analytic method
PROC analytic fibonacci = (INT n)INT:(
REAL sqrt 5 = sqrt(5);
REAL p = (1 + sqrt 5) / 2;
REAL q = 1/p;
ENTIER( (p**n + q**n) / sqrt 5 )
);
FOR i FROM 0 TO 16 WHILE
print(whole(analytic fibonacci(i),0));
# WHILE # i /= 16 DO
print(", ")
OD;
print(new line)
Comments
]]>blog comments powered by Disqus
]]>