Factorial
Calculates and outputs factorials of numbers from 0 to 16, inclusive. Factorial of a number is defined as n! = 1 * 2 * … * n.
Program output should look as follows:
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000
16! = 20922789888000
Note that this example can be implemented in several ways:
- using recursive factorial definition n! = n * (n-1)!
- using multiplication of numbers from 1 to n in a loop.
- using a built-in function of a language.
Example for versions Borland C++ Builder 6, g++ 3.4.5, Microsoft Visual C++ 6, Microsoft Visual C++ 9 (2008)
This example uses recursive factorial definition.
#include "stdio.h"
__int64 factorial(__int64 n)
{
return ( n==0 ? 1 : n*factorial(n-1) );
}
int main(int argc, char* argv[])
{
for (int n=0; n<=16; n++)
printf( "%d! = %I64d\n", n, factorial(n) );
return 0;
}
Example for versions Borland C++ Builder 6, g++ 3.4.5
This example uses recursive factorial definition.
#include <iostream>
unsigned long long factorial(unsigned long long n)
{
if (n == 0)
return 1;
else
return n * factorial (n - 1);
}
int main(void)
{
for (int n = 0; n <= 16; n++)
std::cout << n << "! = " << factorial(n) << std::endl;
return 0;
}
Example for versions Oracle 10g SQL, Oracle 11g SQL
Pure SQL doesn’t support loops, recursions or user-defined functions. This example shows one possible workaround which uses
-
pseudocolumn
levelto construct a pseudotable containing numbers 1 through 16, -
aggregate function
sumwhich allows to sum the elements of a set -
and math functions
expandlnto replace multiplication (required to calculate the factorial) with addition (provided by SQL).
Note that 0! will not be present in the return, since trying to calculate ln(0) produces an exception.
select t2.n || '! = ' || round(exp(sum(ln(t1.n))))
from
( select level n
from dual
connect by level <= 16) t1,
( select level n
from dual
connect by level <= 16) t2
where t1.n<=t2.n
group by t2.n
order by t2.n
Example for versions gcj 3.4.5, Groovy 1.7, Sun Java 6
This example uses recursive factorial definition.
public class Factorial {
static long factorial(int n)
{
return ( n==0 ? 1 : n*factorial(n-1) );
}
public static void main(String[] args)
{
for (int n=0; n<=16; n++)
System.out.println(n+"! = "+factorial(n));
}
}
Example for versions gcj 3.4.5, Groovy 1.7, Sun Java 6
This example uses iterative calculation of factorial and illustrates the use of built-in class BigInteger which allows to handle arbitrarily large integer numbers.
import java.math.BigInteger;
public class Factorial {
public static void main(String[] args)
{
BigInteger f = BigInteger.ONE;
System.out.println("0! = " + f);
for (int n=1; n<=16; n++)
{ f = f.multiply(BigInteger.valueOf(n));
System.out.println( n + "! = " + f);
}
}
}
Example for versions Microsoft SQL Server 2005, Microsoft SQL Server 2008 R2, Microsoft SQL Server 2012
This example uses recursive factorial definition, implemented as a recursive query — a feature included in SQL Server 2005 and higher. Each row of recursive query contains two numeric fields — n and f = n!, and each row is calculated using the data of the previous row.
Note that starting with 2008 version you can calculate factorials only up to 12!. Trying to calculate 13! results in “Data truncation” error, i.e. the resulting value is too large for its datatype.
with factorial(n, f) as
(
select 0, 1
union all
select n+1, f*(n+1) from factorial where n<16
)
select cast(n as varchar)+'! = '+cast(f as varchar)
from factorial
Example for versions EsCo 0.511 (Brainfuck), Müller's Brainfuck 2.0
This example uses iterative definition of factorial. Last calculated factorial is stored in variable c6 and on each step it is multiplied by next number (stored in c5). A low-level description is given in the comments, notation “cXvY” meaning that after execution of the commands in the line the data pointer is at cell X, and the value at this cell is Y. A total of 13 memory cells is used.
This example uses one minor cheat: classic Brainfuck interpreter uses byte variables to store values of memory cells, so 6! and further will cause overflow. Writing long arithmetics in Brainfuck is a bit of overkill, so in this example we assume that memory cells can store integer values. Besides, factorial length grows fast along with execution time of Brainfuck program, so the above code is limited to calculating and printing first 7 factorials.
+++++++++++++++++++++++++++++++++ c1v33 : ASCII code of !
>++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++ c2v61 : ASCII code of =
>++++++++++ c3v10 : ASCII code of EOL
>+++++++ c4v7 : quantity of numbers to be calculated
> c5v0 : current number (one digit)
>+ c6v1 : current value of factorial (up to three digits)
<< c4 : loop counter
[ block : loop to print one line and calculate next
>++++++++++++++++++++++++++++++++++++++++++++++++. c5 : print current number
------------------------------------------------ c5 : back from ASCII to number
<<<<.-.>.<.+ c1 : print !_=_
>>>>> block : print c6 (preserve it)
> c7v0 : service zero
>++++++++++ c8v10 : divizor
<< c6 : back to dividend
[->+>-[>+>>]>[+[-<+>]>+>>]<<<<<<] c6v0 : divmod algo borrowed from esolangs; results in 0 n d_n%d n%d n/d
>[<+>-] c6 : move dividend back to c6 and clear c7
>[-] c8v0 : clear c8
>> block : c10 can have two digits; divide it by ten again
>++++++++++ c11v10: divizor
< c10 : back to dividend
[->-[>+>>]>[+[-<+>]>+>>]<<<<<] c10v0 : another divmod algo borrowed from esolangs; results in 0 d_n%d n%d n/d
>[-] c11v0 : clear c11
>>[++++++++++++++++++++++++++++++++++++++++++++++++.[-]]c13v0 : print nonzero n/d (first digit) and clear c13
<[++++++++++++++++++++++++++++++++++++++++++++++++.[-]] c12v0 : print nonzero n%d (second digit) and clear c12
<<<++++++++++++++++++++++++++++++++++++++++++++++++.[-] c9v0 : print any n%d (last digit) and clear c9
<<<<<<. c3 : EOL
>>+ c5 : increment current number
block : multiply c6 by c5 (don't preserve c6)
>[>>+<<-] c6v0 : move c6 to c8
>> c8v0 : repeat c8 times
[
<<<[>+>+<<-] c5v0 : move c5 to c6 and c7
>>[<<+>>-] c7v0 : move c7 back to c5
>-
]
<<<<- c4 : decrement loop counter
]
Example for versions Interactive FP
This example defines four functions — two of necessity, and two for readability. All of them accept scalar values for input; seq returns a sequence of scalars, and the other three return individual scalars.
-
zerochecks whether its argument is equal to zero; -
decdecrements its argument; -
seqreturns<0>if its argumentxis equal to zero, andseq, applied to(x-1), withxappended to right otherwise (if we unwind this recursive definition, we’ll get simply the sequence of values<0 1 ... x>). -
factorialreturns 1 if its argumentxis equal to zero, andfactorial, applied to(x-1), multiplied byxotherwise.
The last line of the example applies factorial to each element of sequence, obtained by applying seq to 16. Note that all math operations produce floating point values, so the actual output will look like this:
< 1 1.0 2.0 6.0 24.0 120.0 720.0 5040.0 40320.0 362880.0 3628800.0 3.99168E7 4.790016E8 6.2270208E9 8.7178289E10 1.30767428E12 2.09227885E13 >
{ zero ( = @ [id, %0] ) }
{ dec ( - @ [id, %1] ) }
{ seq ( zero -> %<0> ; apndr @ [ seq @ dec , id ] ) }
{ factorial ( zero -> %1 ; * @ [id, factorial @ dec ] ) }
&factorial @ seq:16
Example for versions clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
This example uses recursive factorial definition (which is natural for Lisp). Features:
-
math operators:
(- n 1)is prefix notation equivalent ton-1in infix notation; -
comparison operators:
(= n 0)evaluates toTif n is zero, and tonil(used as false) otherwise; -
conditional operator
if: Lisp expressions are evaluated using brackets, so they can be written in several lines; -
function definition using
defun; -
Common Lisp macro
loop; -
format specifiers in
format:~Dcorresponds to printing an integer, and~%is end-of-line.
(defun factorial (n)
(if (= n 0)
1
(* n (factorial (- n 1))) ) )
(loop for i from 0 to 16
do (format t "~D! = ~D~%" i (factorial i)) )
Example for versions Lua 5.0.3
This example uses recursive factorial definition.
function factorial(n)
if (n == 0) then
return 1
else
return n * factorial(n - 1)
end
end
for n = 0, 16 do
io.write(n, "! = ", factorial(n), "\n")
end
Example for versions Microsoft Visual Basic 6
This example uses iterative factorial definition. Trying to calculate 13! produces an arithmetic overflow error, so program output ends with line “12! = 479001600”. After this a message “Run-time error ‘6’: Overflow” pops up.
Option Explicit
Declare Function AllocConsole Lib "kernel32" () As Long
Declare Function FreeConsole Lib "kernel32" () As Long
Declare Function CloseHandle Lib "kernel32" (ByVal hObject As Long) As Long
Declare Function GetStdHandle Lib "kernel32" (ByVal nStdHandle As Long) As Long
Declare Function WriteConsole Lib "kernel32" Alias "WriteConsoleA" _
(ByVal hConsoleOutput As Long, lpBuffer As Any, ByVal _
nNumberOfCharsToWrite As Long, lpNumberOfCharsWritten As Long, _
lpReserved As Any) As Long
Declare Function Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) As Long
Private Sub Main()
'create a console instance
AllocConsole
'get handle of console output
Dim hOut As Long
hOut = GetStdHandle(-11&)
'output string to console output
Dim s As String
Dim i As Integer
Dim f As Long
f = 1
s = "0! = 1" & vbCrLf
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
For i = 1 To 16 Step 1
f = f * i
s = i & "! = " & f & vbCrLf
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
Next i
'make a pause to look at the output
Sleep 2000
'close the handle and destroy the console
CloseHandle hOut
FreeConsole
End Sub
Example for versions QBasic 1.1, QuickBASIC 4.5
This example uses recursive factorial definition.
The default data type for calculations is floating point, so program output looks like this:
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 3.99168Е+07
12! = 4.790016Е+08
13! = 6.227021Е+09
14! = 8.717829Е+10
15! = 1.307674Е+12
16! = 2.092279Е+13
DECLARE FUNCTION factorial (n)
FOR i = 0 TO 16:
PRINT STR$(i) + "! =" + STR$(factorial(i))
NEXT i
END
FUNCTION factorial (n)
IF n = 0 THEN
factorial = 1
ELSE
factorial = n * factorial(n - 1)
END IF
END FUNCTION
Example for versions Visual Prolog 7.2
Create a new project with UI Strategy “Console” and replace contents of files main.cl and main.pro with given code.
In main.cl the only added line factorial : (integer N, integer F) procedure (i,o). specifies that factorial is a predicate of arity 2, with known first and unknown second argument. Keyword procedure describes the behavior of predicate, indicating that is will always succeed with only one solution, so no backtracking is required.
In main.pro the actual description of newly specified predicate takes place. There are two possible matches for each call of factorial — with zero or arbitrary first argument. Visual Prolog searches the clauses for matching call in the order of their appearance in the code, so if first argument is zero, it starts with first clause factorial(0,F). The first rule in this clause is !, a so-called cut, which prevents backtracking to second clause factorial(N,F) and thus ensures that there is only one solution to the call. After this the return variable F is set to 0! = 1 and the result of the clause is printed. The second clause factorial(N,F) recursively calculates F1 as factorial of N-1, assigns N*F1 to return variable F and prints the result. Finally, stdio::nl prints a new line.
When the main program runs, factorial is called exactly once, for N=12. With each call of recursion N is decremented until it reaches 0. After this factorials are returned and printed in increasing order of N. This program can process only factorials up to 12!, since trying to calculate 13! causes an integer overflow.
% main.cl
class main
open core
predicates
classInfo : core::classInfo.
factorial : (integer N, integer F) procedure (i,o).
predicates
run : core::runnable.
end class main
% main.pro
implement main
open core
constants
className = "main".
classVersion = "".
clauses
classInfo(className, classVersion).
factorial(0,F) :-
!,
F = 1,
stdio::write("0! = 1"),
stdio::nl.
factorial(N,F) :-
factorial(N-1,F1),
F = N*F1,
stdio::write(N, "! = ", F),
stdio::nl.
clauses
run():-
console::init(),
factorial(12,F),
programControl::sleep(1000),
succeed().
end implement main
goal
mainExe::run(main::run).
Example for versions gnuplot 4.2.2
This example consists of two files: factorial.gp and run.gp to emulate loop through use of load, reread and if.
Built-in factorial operator ! is used.
Since return of ! operator has type real, function gprintf is used to remove trailing zeros after decimal point and decimal point itself.
### factorial.gp
print a, '! = ', gprintf("%.0f", a!)
a = a + 1
if (a <= 16) reread
### run.gp
#!/usr/bin/env gnuplot
a = 0
load "factorial.gp"
Example for versions Oracle 10g SQL, Oracle 11g SQL
This example shows the use of model clause, available since Oracle 10g. It allows array-like processing of query rows. Each row has two columns — iteration number (stored in n) and its factorial (stored in f).
select n || '! = ' || f factorial
from dual
model
return all rows
dimension by ( 0 d )
measures ( 0 f, 1 n )
rules iterate (17)
( f[iteration_number] = decode(iteration_number, 0, 1, f[iteration_number-1]*iteration_number),
n[iteration_number] = iteration_number
);
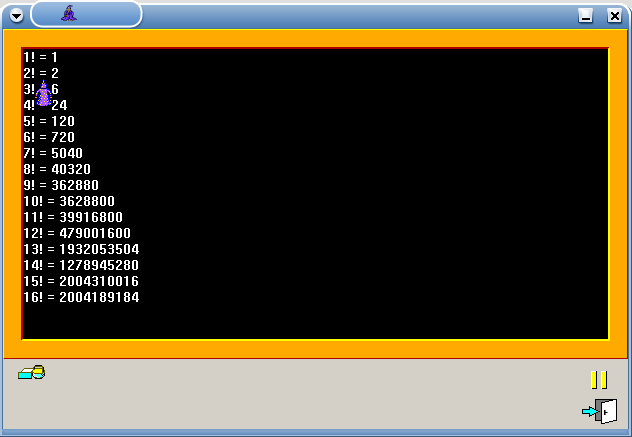
Example for versions Free Pascal 2.0.4, Free Pascal 2.2.0, gpc 20070904, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 5.5, Turbo Pascal 6.0, Turbo Pascal 7.0
This example uses recursive factorial definition.
Note that this example works in all given implementations of Pascal, but it produces slightly different results. In gpc everything works perfectly. Turbo Pascal and Free Pascal have arithmetic overflow for factorial of numbers greater than 12, but Free Pascal reports an error:
13! = Runtime error 215 at $004013C7
$004013C7
$00401449
$004063E0
while Turbo Pascal doesn’t detect the error and simply prints wrong values:
13! = 1932053504
14! = 1278945280
15! = 2004310016
16! = 2004189184
This example doesn’t work in Turbo Pascal 3.0 and earlier due to absence of longint data type in these versions.
In GNU Pascal this program works without any problems.
program factorial;
function fact(n: integer): longint;
begin
if (n = 0) then
fact := 1
else
fact := n * fact(n - 1);
end;
var
n: integer;
begin
for n := 0 to 16 do
writeln(n, '! = ', fact(n));
end.
Example for versions MySQL 3.23.57
Replace TABLE with name of any table you have access to, like mysql.help_topic.
select concat(cast(t2.n as char), "! = ", cast(exp(sum(log(t1.n))) as char))
from
( select @i := @i+1 AS n
from TABLE, (select @i := 0) as sel1
limit 16 ) t1,
( select @j := @j+1 AS n
from TABLE, (select @j := 0) as sel1
limit 16 ) t2
where t1.n <= t2.n
group by t2.n
Example for versions Bash 3.0, Bash 4.0.35
This example uses recursive factorial definition.
factorial ()
{
local num=$1;
if [ $num = 0 ]; then
echo 1
return ;
fi;
echo $(( $num * $(factorial $(( $num - 1 )) ) ))
}
for ((n = 0; n <= 16; n++))
do
echo "$n! = " $(factorial $(($n)))
done
Example for versions Poplog 15.5 (Prolog)
This example consists of two parts — the first part of code should be stored in a file fact.pl placed in working folder of Poplog, and the second one has to be entered manually. [-fact]. downloads facts and rules from this file to current Prolog session (and outputs fact reconsulted to note that download succeeded). Query fact(16,X). tries to find value of X for which this predicate will evaluate to true. The output required in the example is side effect of query evaluation, and the actual result will be X = 20922789888000 ?. This means that if you’re not satisfied with this binding, you can reject it (by entering ;), and the search for better binding will continue.
% fact.pl
fact(X, F) :-
( X=0, F=1;
Y is X-1, fact(Y, Z), F is X*Z),
write(X), write('! = '), write(F), nl.
% interactive
[-fact].
fact(16,X).
Example for versions Python 2.5.2, Python 2.6.5
This example uses recursive factorial definition.
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
for n in range(16 + 1):
print "%d! = %d" % (n, factorial(n))
Example for versions ARIBAS 1.53
This example uses built-in factorial function.
ARIBAS uses integer type for variables by default, so type declaration can be omitted.
group(0) is used to cancel digit groups separation by underscores during output.
function fac0_16();
var n;
begin
for n := 0 to 16 do
writeln(n, "! = ", factorial(n): group(0));
end;
end;
fac0_16().
Example for versions ARIBAS 1.53
This example uses recursive factorial definition.
Function name fac is used because factorial is reserved function name in ARIBAS.
ARIBAS uses integer type for variables by default, so type declaration can be omitted.
group(0) is used to cancel digit groups separation by underscores during output.
function fac(n);
begin
if (n = 0) then
return(1);
end;
return(n * fac(n - 1));
end;
function fac0_16();
var n;
begin
for n := 0 to 16 do
writeln(n, "! = ", fac(n): group(0));
end;
end;
fac0_16().
Example for versions PHP 5.2.4, PHP 5.3.2
This example uses recursive factorial definition.
<?php
function factorial($n)
{
if ($n == 0) {
return 1;
}
return $n * factorial($n - 1);
}
for ($n = 0; $n <= 16; $n++) {
echo $n . "! = " . factorial($n) . "\n";
}
?>
Example for versions Ruby 1.8.5
This example uses recursive factorial definition.
#! /usr/bin/env ruby
def factorial(n)
if n == 0
1
else
n * factorial(n - 1)
end
end
0.upto(16) do |n|
print(n, "! = ", factorial(n), "\n")
end
Example for versions Microsoft Visual Basic .NET 9 (2008), vbnc 2.4.2
This example uses recursive factorial definition.
Module Module1
Function Factorial(ByVal n As Integer) As Long
If n = 0 Then
Return 1
Else
Return n * Factorial(n - 1)
End If
End Function
Sub Main()
For i As Integer = 0 To 16
Console.WriteLine(i & "! = " & Factorial(i))
Next
End Sub
End Module
Example for versions gcc 3.4.5, gcc 3.4.5 (Objective-C), gcc 4.2.4, tcc 0.9.25
This example uses recursive factorial definition. Note that 13! and larger causes an overflow, so the last lines of the output look like this:
13! = 1932053504
14! = 1278945280
15! = 2004310016
16! = 2004189184
#include <stdio.h>
unsigned long long factorial(unsigned long long n)
{
if (n == 0) {
return 1;
} else {
return n * factorial (n - 1);
}
}
int main(void)
{
int n;
for (n = 0; n <= 16; n++) {
printf("%i! = %lld\n", n, factorial(n));
}
return 0;
}
Example for versions gmcs 2.0.1, Microsoft Visual C# 2008
This example uses recursive factorial definition.
using System;
class Program
{
static long Factorial(int n)
{
if (n == 0)
return 1;
else
return n * Factorial(n - 1);
}
static void Main(string[] args)
{
for (int i = 0; i < 17; i++)
Console.WriteLine("{0}! = {1}",i,Factorial(i));
}
}
Example for versions Poplog 15.5 (POP-11)
This example uses recursive factorial definition. factorial(n) calculates the actual value of factorial, while loop(n) is used to loop through factorials of numbers between 0 and n, inclusive. >< is concatenation operator. Note that loop doesn’t return a value.
Alternatively, one could save function definitions to file fact.p, place it in Poplog working folder, and enter load fact.p in interactive mode to upload the contents of file.
define factorial(n);
if n == 0
then 1
else n * factorial(n - 1)
endif
enddefine;
define loop(n);
if n>0
then loop(n-1)
endif;
n >< '! = ' >< factorial(n) =>
enddefine;
loop(16) =>
Example for versions rakudo-2010.08
This version uses the reduction metaoperator to multiply every number from 1 to N (the leading [*] means “apply the * operator between each element of the following list”).
Note that the say statement could also be written as:
say "$i! = &fact($i)";
with the function call interpolated directly into the string being printed.
sub fact($n) { [*] 1..$n }
for 0..16 -> $i {
say "$i! = ", fact($i);
}
Example for versions Euphoria v3.1.1, Euphoria v4
This example uses recursive factorial definition.
function factorial(integer n)
atom result
if n <= 1 then
result = 1
else
result = n * factorial(n-1)
end if
return result
end function
for i = 0 to 16 do
printf(1, "%d! = %d\n", {i, factorial(i)})
end for
Example for versions Euphoria v3.1.1, Euphoria v4
This example uses iterative factorial definition.
function factorial(integer n)
atom result = 1
if n < 1 then
return 1
end if
for i = 2 to n do
result *= i
end for
return result
end function
for i = 0 to 16 do
printf(1, "%d! = %d\n", {i, factorial(i)})
end for
Example for versions Oracle 10g SQL, Oracle 11g SQL
This example calculates factorials iteratively by means of PL/SQL.
declare
n number := 0;
f number := 1;
begin
while (n<=16)
loop
dbms_output.put_line(n || '! = ' || f);
n := n+1;
f := f*n;
end loop;
end;
Example for versions Squeak 3.10
This example is actually cut and paste from the Squeak core source code in the Integer class. From any Squeak image:
10000 factorial. “and press alt-p to print the result below this line”
284625968091705451890641321211986889014805140170279923079417999427441134000376444377299078675778477581588406214231752883004233994015351873905242116138271617481982419982759241828925978789812425312059465996259867065601615720360323979263287367170557419759620994797203461536981…etc… edited for brevity.
This takes about 200 milliseconds on a modern PC to compute the factorial, and about 6 seconds to convert the resulting number into a String for displaying.
The resulting number has this 35660 digits:
10000 factorial asString size
35660
factorial
"Answer the factorial of the receiver."
self = 0 ifTrue: [^ 1].
self > 0 ifTrue: [^ self * (self - 1) factorial].
self error: 'Not valid for negative integers'
Example for versions Free Pascal 2.0.4, Free Pascal 2.2.0, gpc 20070904, Turbo Pascal 1.0, Turbo Pascal 2.0, Turbo Pascal 3.0, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 5.5, Turbo Pascal 6.0, Turbo Pascal 7.0
This example is exactly the same as main recursive example for Pascal implementations, except for that it uses real data type to store factorial values. Command writeln(f:-1:0) outputs the floating point number f with 0 digits after decimal point and left-justifies it.
program factorial;
function fact(n: integer): real;
begin
if (n = 0) then
fact := 1
else
fact := n * fact(n - 1);
end;
var
n: integer;
begin
for n := 0 to 16 do
writeln(n, '! = ', fact(n):-1:0);
end.
Example for versions REXX
This example uses recursive factorial definition.
Line 3: REXX allows the numeric precision to be set arbitrarily large — as much as your memory will allow.
Line 6: String concatenation works by juxtaposing values and literals, with or without intervening spaces. If two values must be concatenated, the || operator can be used.
Line 10: The optional PROCEDURE keyword causes the routine’s variables to be local; without it they are global to the program.
The output looks as follows:
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000
16! = 20922789888000
17! = 355687428096000
18! = 6402373705728000
19! = 121645100408832000
20! = 2432902008176640000
21! = 51090942171709440000
22! = 1124000727777607680000
23! = 25852016738884976640000
24! = 620448401733239439360000
25! = 15511210043330985984000000
26! = 403291461126605635584000000
27! = 10888869450418352160768000000
28! = 304888344611713860501504000000
29! = 8841761993739701954543616000000
30! = 265252859812191058636308480000000
1 #!/usr/bin/rexx
2 /* Compute n! */
3 numeric digits 40
4
5 do n = 0 to 30
6 say right(n,2)"! = " right(factorial(n),35)
7 end
8 exit
9
10 factorial: procedure
11 parse arg n .
12
13 if n = 0 then
14 n = 1
15
16 else
17 n = n * factorial(n - 1)
18 return n
Example for versions D1, D2, gdc 0.24
This example uses recursive factorial definition.
module factorial;
import std.stdio;
ulong recursive(ulong x)
{
return (x == 0 ? 1 : x * recursive( x - 1 ));
}
int main()
{
for (int i = 0; i < 17; ++i)
{
writefln("%s! = %s", i, recursive(i));
}
return 0;
}
Example for versions j602
This example implements three methods of calculating factorial. fact represents a factorial function which generates the first n integers as an array and multiplies them together. factr represents the recursive definition. ! is the built-in factorial function.
load 'printf'
fact=: [: */ [: >: i.
factr=: 1:`(]*$:@<:)@.*
'!%d = %d' printf (,"0 fact) i.17x
'!%d = %d' printf (,"0 factr) i.17x
'!%d = %d' printf (,"0 !) i.17x
Example for versions Algol68g-1.18.0, Algol68toc-1.8
This example uses recursive factorial definition with first 7 numbers precomputed.
PROC factorial = (INT n)LONG LONG INT:
CASE n+1 IN
1,1,2,6,24,120,720 # a brief lookup #
OUT
n*factorial(n-1)
ESAC
;
Example for versions gfortran 4.5.0, Intel Visual Fortran 11.1
This example uses iterative factorial definition. Format specifiers I and A are used for printing integers and strings, respectively. Trying to calculate 13! produces an arithmetic overflow error, so last lines of program output look like this:
13! = 1932053504
14! = 1278945280
15! = 2004310016
16! = 2004189184
program Factorial
integer :: f,n
f = 1
n = 0
do
print '(I2, A, I10)', n, "! = ", f
n = n + 1
f = f * n
if (n==17) then
exit
end if
end do
end program Factorial
Example for versions OCaml 3.11
This example uses an auxiliary function fact, so that tail recursion is possible.
let rec fact n accum =
if n <= 1 then
accum
else
fact (n-1) (accum*n);;
let factorial n =
fact n 1;;
let () =
for n = 0 to 16 do
Printf.printf "%d! = %d\n" n (factorial n)
done;
Example for versions OCaml 3.11
This example shows the naive way to implement the factorial function. However, it is not tail recursive, since the recursive function call is not the only statement on the line.
let rec factorial n =
if n <= 1 then
1
else
factorial (n-1) * n;;
let () =
for n = 0 to 16 do
Printf.printf "%d! = %d\n" n (factorial n)
done;
Example for versions SpiderMonkey 1.7
This example uses recursive factorial definition and is meant to be executed from the web-browser. To run the example, copy its source text to a file factorial.js and create an HTML file placed in the same directory and containing the following text:
<head><script type="text/javascript" src="factorial.js"></script></head>
<body></body>
When you open the HTML file, JavaScript code runs and writes its output to the page shown. document.clear() command clears everything that is written on the currrent web-page.
function factorial(n)
{ if (n == 0)
return 1;
else
return n * factorial(n-1);
}
var i;
document.clear();
for (i = 0; i <= 16; i++)
document.write(i + "! = " + factorial(i) + "<br />");
Example for versions GHC 6.10.4
This example uses recursive factorial definition and consists of three major parts:
-
definition of
factorialfunction, which takes one argument ofIntegertype (integer number of unlimited precision) and returns the same type. The function is defined recursively, and types of argument and return are given explicitly to avoid ambiguity. -
definition of
linefunction, which prints the number and its factorial in required format. Use of
printfcommand is the same as in C++. -
printing the numbers and their factorials themselves.
[0..16]creates a list of numbers from 0 to 16, inclusive. Functionmapapplies first argument (linefunction) to each element of second argument ([0..16]list) and as a result creates a list of so-called “output actions” (which can be used as values in Haskell). To combine these actions in one we usesequence_command, which is applied to a list of actions, executes first action from the list and recursively applies it to the tail of the list. But for simplicity, we usemapM_, which combinesmapandsequence_.
module Main where
import Text.Printf
factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n - 1)
line x = printf "%d! = %d\n" x $ factorial x
main = mapM_ line [0..16]
Example for versions clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
In this example the inner loop with collect clause produces a list of numbers from 1 to n. After this operation * is applied to this list, and the product of the numbers is printed.
(loop for n from 0 to 16
do (format t "~D! = ~D~%" n
(apply '* (loop for i from 1 to n
collect i)) ) )
Example for versions Furry Paws
This example works in exactly the same way as the one in Interactive FP, except for that it doesn’t define zero function, since it’s built-in. Note that here all operations are done within integer data type, and 13! overflows it, so the program can be called only to print factorials up to 12!. show is another way to output data.
dec = sub.[id, ~1]
seq = zero -> [id] ; cat.[seq.dec, [id]]
factorial = zero -> ~1 ; mul.[id, factorial.dec]
main = show.(return @factorial.(seq.~12))
Example for versions gnat 3.4.5, gnat 4.3.2
This example uses recursive factorial definition.
Note that there are different packages for printing text, integers and long integers. put command generally accepts several arguments: Item is the number/string to print, Width is the number of positions to use, Fore and Aft are the numbers of decimal digits to be printed before and after decimal separator etc. If there is only one argument, it is considered to be Item. Setting Width to a number which is less than the actual length of the number prints it without leading spaces (which is the default for Ada).
Another thing to note is that Ada doesn’t support implicit data type conversions, so to calculate N*Fact(N-1) one has to convert N to Long_Long_Integer explicitly first.
with Ada.Text_IO, Ada.Integer_Text_IO, Ada.Long_Long_Integer_Text_IO;
procedure Factorial is
begin
declare
function Fact (N: Integer) return Long_Long_Integer is
begin
if N=0 then
return 1;
else
return Long_Long_Integer(N)*Fact(N-1);
end if;
end Fact;
i: Integer := 0;
begin
loop
Ada.Integer_Text_IO.Put (Item => i, Width => 1);
Ada.Text_IO.Put ("! = ");
Ada.Long_Long_Integer_Text_IO.Put (Item => Fact(i), Width => 1);
Ada.Text_IO.New_Line;
i := i + 1;
exit when i=17;
end loop;
end;
end Factorial;
Example for versions Scratch 1.4
Since Scratch is a graphical language, the print-screen contains the actual information about the program, source text is only a transcription.
strs is a vector-style array. delete all block is required to clean it before running program again. repeat is a kind of loop which repeats its body for exactly the given number of times. join is a block which concatenates its arguments. hide hides the avatar (to clean the stage).
Scratch doesn’t have a standard output as such, neither has it a possibility of “saying” multi-line things. An array was used to output the example results in the required form.
delete all of strs
set i to 0
set f to 1
repeat 17
add (join i (join (! = ) f)) to strs
set i to (i + 1)
set f to (f * i)
hide
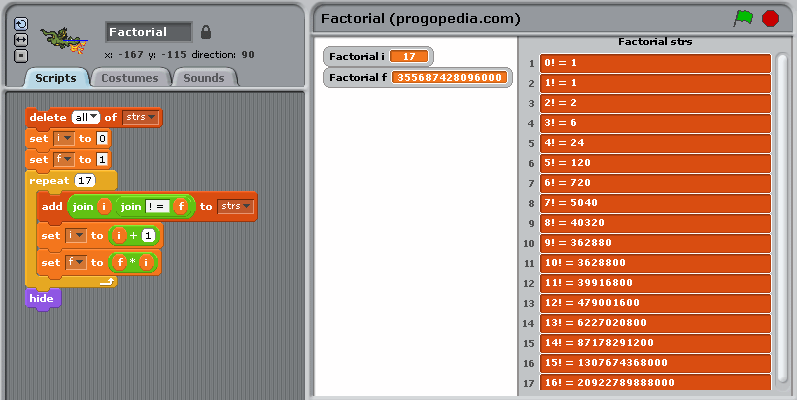
Factorial example in Scratch
Example for versions UCBLogo 6.0
This example uses recursive factorial definition. It defines two functions — factorial which calculates N! and print_factorial which loops through numbers from i to N and outputs their factorials.
to factorial :N
ifelse :N = 0 [output 1] [output :N * factorial :N - 1]
end
to print_factorial :i :N
repeat :N - :i + 1 [(print :i [! =] factorial :i)
make "i sum :i 1]
end
print_factorial 0 16
Example for versions gc-2010-07-14
The example implements both recursive and iterative methods of calculating factorial and a generic function for printing the results of using any of the methods.
package main
import "fmt"
//Recursive Factorial
func factr(n uint64) uint64 {
if (n < 2) { return 1 }
return n * factr(n-1)
}
//Iterative Factorial
func facti(n uint64) uint64 {
var ret uint64 = 1
for ; n > 0; n-- {
ret *= n
}
return ret
}
func printFact(fact func(uint64) uint64) {
for i := 0; i < 17; i++ {
fmt.Printf("%d! = %d\n", i, fact(uint64(i)))
}
}
func main() {
printFact(factr)
fmt.Println("--")
printFact(facti)
}
Example for versions Ruby 1.8.5
This example uses an iterative factorial definition.
def fact(n)
(1..n).inject(1) {|a,b| a*b}
end
(0..16).each {|x| puts "#{x}! = #{fact(x)}"}
Example for versions D1, D2, gdc 0.24
This example uses iterative factorial definition. Note the usage of foreach loop.
module factorial;
import std.stdio;
ulong iterative(ulong x) {
ulong result = 1;
foreach (ulong count; 1..x+1)
result *= count;
return result;
}
int main() {
foreach (int i; 0..17)
writefln("%s! = %s", i, iterative(i));
return 0;
}
Example for versions Scala 2.7.7-final
This example uses recursive factorial definition.
object Factorial {
def factorial(n: Int): Long =
if (n == 0) 1
else n * factorial(n - 1)
def main(args: Array[String]) {
for {i <- List.range(0, 17)}
yield { println(i + "! = " + factorial(i)) }
}
}
Example for versions Scala 2.7.7-final
This example uses iterative factorial definition.
object Factorial {
def main(args: Array[String]) {
var f = BigInt(1)
format("0! = %s\n", f)
for {i <- 1 to 16} {
f *= i;
format("%s! = %s\n", i, f)
}
}
}
Example for versions gawk 3.1.6, Jawk 1.02, mawk 1.3.3
This example uses iterative factorial definition. Individual statements within code block can be separated with semicolons (;) or new lines.
BEGIN {
f = 1
print "0! = " f
for (i=1; i<17; i++) {
f *= i
print i "! = " f
}
}
Example for versions GHC 6.10.4
This example uses the Prelude function product, which computes the product of a list of numbers. When the list is empty, it returns 1 (the multiplicative identity), so this works for 0 too.
module Main where
factorial :: Integer -> Integer
factorial n = product [1..n]
line x = putStrLn $ show x ++ "! = " ++ factorial x
main = mapM_ line [0..16]
Example for versions GHC 6.10.4
This example performs a “fold” using the function foldl (which is a left-fold, but since multiplication is associative, left fold and right fold are the same) to fold multiplication over the list [1..n]. We provide the “initial value” 1, so that it will produce 1 when the list is empty.
module Main where
factorial :: Integer -> Integer
factorial n = foldl (*) 1 [1..n]
line x = putStrLn $ show x ++ "! = " ++ factorial x
main = mapM_ line [0..16]
Example for versions perl 5.8.8
This example uses the reduce function from the List::Util module. Note that we have to put an extra 1 in the beginning, so that it will work when 1 .. $n is empty (i.e. when $n is 0).
use List::Util qw(reduce);
sub fact {
my $n = shift;
reduce { $a * $b } 1, 1 .. $n
}
foreach my $i (0..16) {
print "$i! = ", fact($i), "\n";
}
Example for versions perl 5.8.8
This example uses recursive factorial definition.
sub fact {
my $n = shift;
$n == 0 ? 1 : $n*fact($n-1);
}
foreach my $i (0..16) {
print "$i! = ", fact($i), "\n";
}
Example for versions perl 5.8.8
This example uses iterative factorial definition.
sub fact {
my $n = shift;
my $result = 1;
foreach my $i (1 .. $n) {
$result *= $i;
}
$result
}
foreach my $i (0..16) {
print "$i! = ", fact($i), "\n";
}
Example for versions S-lang 2.2.2
This example uses recursive factorial definition and features the usage of recursive functions in S-lang. To create a recursive function, you have first to declare it without listing parameters or implementation — define factorial ();, and then actually define it, with the list of parameters and function body.
Another feature included in this example is usage of $ suffix. A string literal can end with a suffix which defines the way of processing this string. $ suffix requires that variable name substitution is performed on the string before using it. This means that each variable name prefixed by $ character within the string will be replaced with variable value. Variable name can be enclosed in {} braces to separate it from the string contents; the braces can be omitted if variable name is followed by a space.
Note that the default numeric data type in S-lang is integer, so the given example produces overflow error when calculating 13!.
define factorial ();
define factorial (n)
{ if (n==0) return 1;
return n * factorial (n-1);
};
for (i=0; i<17; i++)
{ f = factorial (i);
message ("${i}! = ${f}"$);
};
Example for versions S-lang 2.2.2
This example shows array operations in S-lang. [1:i] creates a list of numbers from 1 to i; note that the default data type for array operations is double even if the numbers are integer. Intrinsic function prod (since version 2.1) returns the product of elements of its parameter. Intrinsic function sprintf provides C-style printing, %.0f printing floating point number with zero digits after decimal comma.
for (i=0; i<17; i++)
sprintf ("%d! = %.0f", i, prod ( [1:i] ) );
Example for versions Sanscript 2.2
Sanscript is a fully visual programming language, so no source code is available. See screeshots instead.
First screenshot shows the flowgram of the example. The main part of it is “Repeat” function (an analogue of loop in other languages) which calculates the factorials of numbers from 1 to 16 and stores them in a list. This function has two inlet/outlet pairs which correspond to global variables in other languages: factorial and message. factorial is an integer which stores the current value of factorial. message is a list of text lines n! = (n!). The “Repeat” function has one more inlet N which defines the number of iterations to be done. The inlets are initialized with constants and an empty list, and the loop starts. Once the calculations are done, message has to be displayed. This can be done using Write List as Text function, which writes all elements of list into a single text variable. The separator between elements of the list is defined with sep inlet; in this case it is newline character, generated using “Char” function which converts an ASCII-code into a corresponding character. Finally, the concatenated list is displayed using “Display Message” function.
Second screenshot shows the intrinsics of “Repeat” function. Element marked with “1, 2 …” is loop counter, started with 1 and incremented by 1 each iteration. On each iteration factorial is multiplied by the value of loop counter (using “Times” function). After this its new value is concatenated with loop counter and “! = ” constant string (using “Append Text” function) to produce one line of output. Finally, this line is added to the list message (using “Add Last Item”) function.
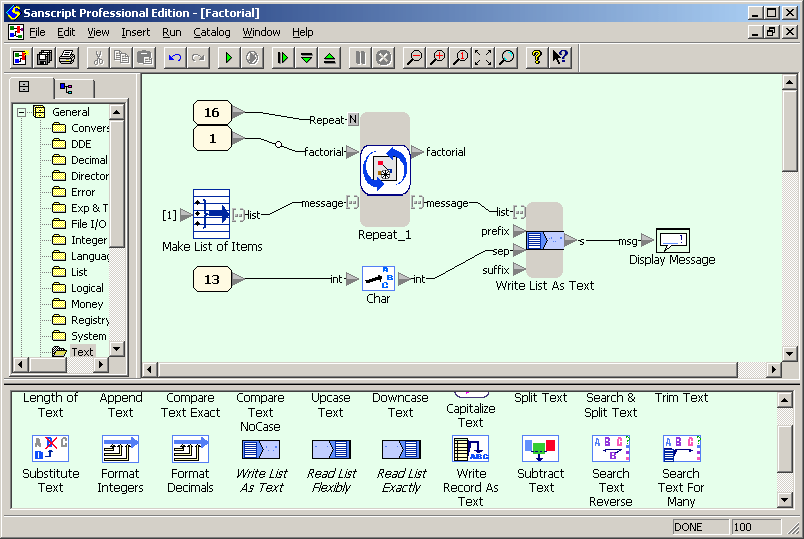
Factorial example in Sanscript (flowgram)
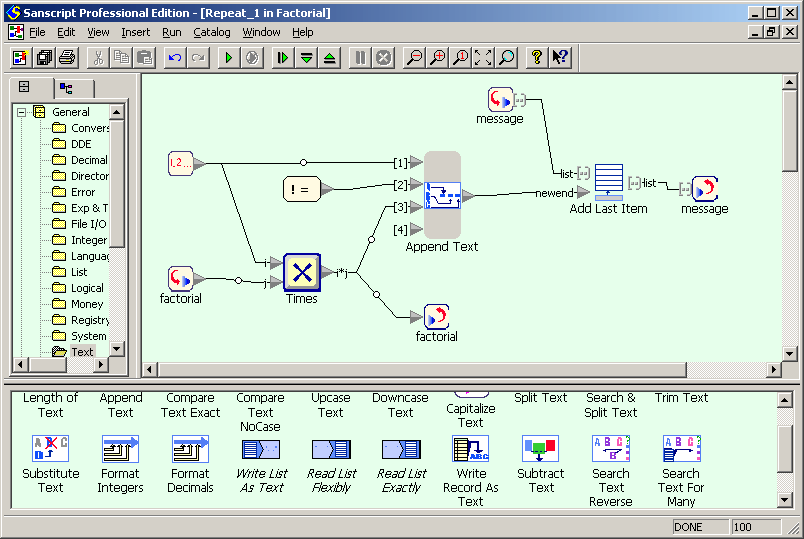
Factorial example in Sanscript (repeat)
Example for versions Ruby 1.9
This example uses an iterative factorial definition
def fact(n)
(1..n).reduce(:*)
end
(0..16).each {|x| puts "#{x}! = #{fact(x)}"}
Example for versions Simply Scala
This examples shows how to define ! as a method applied to Int.
def factorial(n: Int): BigInt =
if (n == 0) 1
else factorial(n - 1) * n
class Factorizer(n: Int) {
def ! = factorial(n)
}
implicit def int2fact(n: Int) = new Factorizer(n);
for {i <- List.range(0, 17)}
println(i + "! = " + (i!))
Example for versions Roco 20071014
This example uses iterative definition of factorial. Cell [0] stores the current number, cell [1] is temporary, and cell [2] stores factorial of current number.
co calc{
/* break the loop when the counter is 17 - the number for which we don't need factorial */
eq [1] [0] 17
if [1] ac
/* output current factorial */
iout [0]
cout 33
cout 32
cout 61
cout 32
iout [2]
cout 13
cout 10
/* calculate next number and store it to [2]*/
add [0] [0] 1
mul [2] [2] [0]
}
/* initialize with 0! = 1 */
set [0] 0
set [2] 1
ca calc
ac
Example for versions fsharp 2.0.0
This example uses recursive definition of factorial, expressed in procedural paradigm.
factorial defines the actual factorial-calculating routine, and printFact defines the routine that outputs calculated factorials in required format.
let rec factorial n =
match n with
| 0 -> 1
| _ -> n * factorial (n - 1)
let rec printFact n =
match n with
| 0 -> printfn "0! = 1"
| _ -> printFact (n-1)
printfn "%d! = %d" n (factorial (n))
printFact(16)
Example for versions FP trivia 20210108
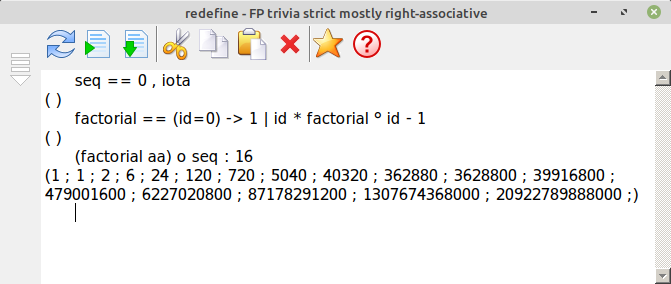
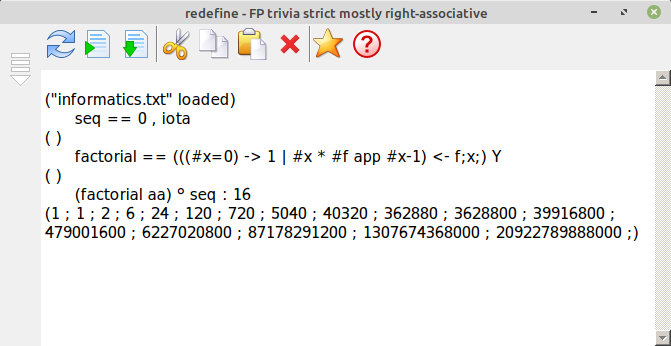
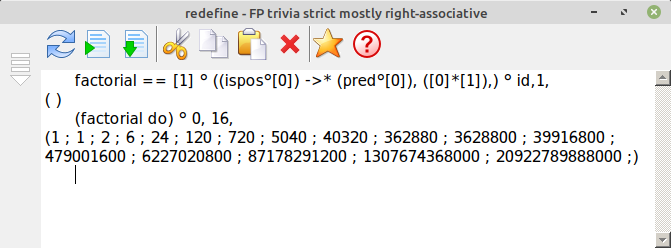
This example provides a list of factorials from 0 up to 16. Factorial for a non-recursive / recursive version.
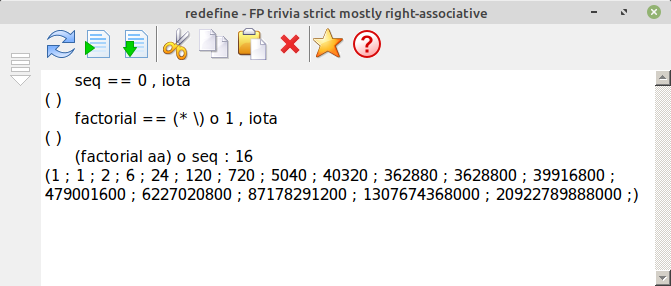
Factorial non-recursive
Factorial recursive
Factorial with Y combinator
Factorial with while- and for-do-loop
Example for versions Bash 4.0.35
This example uses iterative factorial definition.
f=1
for (( n=1; $n<=17; $((n++)) ));
do
echo "$((n-1))! = $f"
f=$((f*n))
done
Example for versions Miller's Hack VM (JavaScript), Miller's Hack VM (Python)
This example is pretty similar to Fibonacci numbers one, just with more characters to output. Note that data type is 32-bit integers, so 13! overflows: the output look like this:
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
!ERROR: integer overflow
28*0> 56*3+1> 84*2> 78*5+3> 25*4> 05> 16> 5<p1<P2<P3<P2<P6<p4<P 5<1+5> 5<6<*6> 0<1-0> 0<6? 67*c
Example for versions Whitespacers (Ruby)
This example uses a slightly different method of commenting — each command is preceded with its literal description. Numbers and labels are enclosed in brackets.
The example works as follows: heap is used to store variables (1 — index of the first factorial which doesn’t need to be calculated, 2..5 — ASCII-codes of special characters used in printing, 6 and 7 — current number and its factorial), and stack is used to run commands). Factorial is calculated iteratively, on each iteration previously calculated values are printed, and new ones are calculated and stored to memory. After this, the newly calculated number is compared with contents of cell 1: if it is less, the loop continues, otherwise it halts.
A curious thing to note is that in Whitespace numeric system zero is “negative”: a number must have at least one Tab in its notation, and binary notation of zero has no 1s, so it has to be written as Tab (only sign bit).
push_1 { }
push_17 { }
store push_2 { }
push_33 { }
store push_3 { }
push_32 { }
store push_4 { }
push_61 { }
store push_5 { }
push_10 { }
store push_6 { }
push_0 { }
store push_7 { }
push_1 { }
store label
{ }
printing_block_push_6 { }
retrieve print_as_number
push_2 { }
retrieve print_as_char
push_3 { }
retrieve print_as_char
push_4 { }
retrieve print_as_char
push_3 { }
retrieve print_as_char
push_7 { }
retrieve print_as_number
push_5 { }
retrieve print_as_char
increase_counter_block_push_6 { }
push_6 { }
retrieve push_1 { }
add store calculate_next_factorial_block_push_7 { }
push_7 { }
retrieve push_6 { }
retrieve multiply
store conditional_return_block_push_6 { }
retrieve push_1 { }
retrieve subtract jump_if_negative
{ }
quit
end
Example for versions QBasic 1.1, QuickBASIC 4.5
This example uses iterative factorial definition. Arithmetic overflow happens when trying to calculate 13!, but different implementations handle it in different ways: QBasic reports an exception, while QuickBasic just proceeds printing negative values.
DIM f AS LONG
f = 1
PRINT " 0 ! ="; f
FOR i = 1 TO 16:
f = f * i:
PRINT i; "! ="; f
NEXT i
END
Example for versions erl 5.7.3
This example uses recursive factorial definition. Note that Erlang has no built-in loops, so the example uses a recursive function which starts with larger values of N, but calls itself for N-1 before printing N!. loop(_) is a clause that defines evaluation of loop() when its argument is not an integer or is negative; it is necessary for a proper function definition.
-module(prog).
-export([main/0, loop/1]).
fact(0) -> 1;
fact(N) -> N * fact(N-1).
loop(N) when is_integer(N), N>=0 ->
loop(N-1),
io:format("~B! = ~B~n",[N,fact(N)]);
loop(_) -> ok.
main() -> loop(16).
Example for versions B-Prolog 7.4 #3, gprolog 1.3.0, swipl 5.6.x
Almost identical to Poplog Prolog example, except for the syntax of compiling a file (doesn’t have a - before file name). However, the results of execution depend on the implementation. SWI-Prolog handles large numbers just fine, while in GNU Prolog and B-Prolog 12! overflows the numeric data type, so all values after 11! are incorrect.
| ?- [fact].
compiling /home/nickolas/Desktop/progopedia/prolog/fact.pl for byte code…
/home/nickolas/Desktop/progopedia/prolog/fact.pl compiled, 3 lines read — 1372 bytes written, 5 ms
yes
| ?- fact(16,X).
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = -57869312
13! = -215430144
14! = 205203456
15! = -143173632
16! = -143294464
X = -143294464 ?`
% fact.pl
fact(X, F) :-
( X=0, F=1;
Y is X-1, fact(Y, Z), F is X*Z),
write(X), write('! = '), write(F), nl.
% interactive
[fact].
fact(16,X).
Example for versions bc 1.06
This example uses recursive factorial definition.
define factorial(n) {
if (n == 0) return(1);
return(n * factorial(n - 1));
}
for (n = 0; n <= 16; n++) {
print n; "! = "; factorial(n);
}
Example for versions boo 0.8.2
This example uses recursive factorial definition. The function factorial is called recursively, so it needs an explicit declaration of its return type.
def factorial(n as long) as long:
if n == 0:
return 1
else:
return n * factorial(n - 1)
for n in range(0, 17):
print("${n}! = ${factorial(n)}")
Example for versions boo 0.8.2
This example uses iterative factorial definition. Variable fact needs an explicit type declaration, since otherwise it will be typed as int, and trying to calculate 13! will cause an overflow error.
fact as long = 1
for i in range(17):
print("${i}! = ${fact}")
fact = fact * (i+1)
Example for versions gforth 0.7.0
This example uses recursive factorial definition. Forth is a stack-oriented language, so all commands (words) perform stack manipulations. Thus, dup duplicates the topmost element of the stack, a constant pushes itself on the top of the stack, > compares second-topmost element to the topmost element and pushes the result, - subtracts topmost element from second-topmost, etc.
: fac recursive
dup 1 > IF
dup 1 - fac *
else
drop 1
endif ;
: lp
swap 1 + swap
do
i . i ." ! = " i fac . cr
loop ;
16 0 lp
Example for versions c-intercal 28.0, J-INTERCAL 0.11, J-INTERCAL 0.12
This example uses iterative factorial definition. The looping part is similar to Fibonacci example, the body differs, but only a little bit. Note usage of : prefix for variables instead of . — the former means 32-bit variables, and the latter — 16-bit ones. The output looks as follows (numbers go in pairs, n and n!, and each number takes two lines to be written):
_
I
I
I
II
II
III
VI
IV
XXIV
V
CXX
VI
DCCXX
VII
_
VXL
VIII
__
XLCCCXX
IX
_____
CCCLXMMDCCCLXXX
X
___________
MMMDCXXVIIIDCCC
XI
_____
xxxixCMXVIDCCC
XII
cdlxxixMDC
XIII
___
mcmxxxMMLMMMDIV
XIV
_____
mcclxxviiiCMXLVCCLXXX
XV
____
mmivCCCXXVI
XVI
_______
mmivCLXXXIXCLXXXIV
C-INTERCAL uses Roman notation, in which a bar over a numeral multiplies its value by 1000, and writing a letter in lowercase multiplies its value by 1000000.
DO .9 <- #17
DO :10 <- #0
DO :11 <- #1
DO :2 <- :10
(1) PLEASE READ OUT :10
PLEASE READ OUT :11
DO :1 <- #1
PLEASE (1509) NEXT
DO :10 <- :3
DO :2 <- :10
DO :1 <- :11
PLEASE (1549) NEXT
DO :11 <- :3
DO (3) NEXT
DO (1) NEXT
(3) DO (4) NEXT
PLEASE GIVE UP
(4) DO .1 <- .9
DO .2 <- #1
PLEASE (1010) NEXT
DO .9 <- .3
DO .1 <- '.9~.9'~#1
PLEASE (1020) NEXT
DO RESUME .1
Example for versions Mozart 1.4.0
This example uses iterative factorial definition. Compile using ozc -x <filename>.
functor
import
Application System
define
local
F
in
F = {NewCell 1}
for I in 0..16 do
{System.showInfo {Append {Append {Int.toString I} "! = "} {Int.toString @F}}}
F := (I+1) * @F
end
{Application.exit 0}
end
end
Example for versions gst 3.1
Smalltalk provides built-in factorial method of class Number, so the example is really simple.
0 to: 16 do: [ :i |
i display.
'! = ' display.
i factorial displayNl
].
Example for versions ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
This example uses iterative factorial definition. In Tcl 8.4 values of factorials starting with 13! are calculated incorrectly due to overflow. In later versions and other implementations all values are correct.
set fact 1
for {set i 0} {$i <= 16} {incr i} {
puts "$i! = $fact"
set fact [expr {$fact * ($i + 1)}]
}
Example for versions ncc 0.9.3
This example uses recursive factorial definition; tail recursion is optimized by the compiler to become a loop. Note that the default data type is int, so trying to calculate 13! results in overflow error:
Unhandled Exception: System.OverflowException: Number overflow.
def fact(i)
{
| 0 => 1
| other => other * fact(other - 1)
}
for (mutable i=0; i<16; i++)
System.Console.WriteLine("{0}! = {1}", i, fact(i));
Example for versions Web2c 2009
This example uses iterative factorial definition.
Note that \factorial macro has to use double curly brackets because it has loop that is used inside other loop.
Also only factorials up to 12 are handled. For bigger numbers TeX throws “Arithmetic overflow” error.
\newcount\n \newcount\p \newcount\m
\def\factorial#1{{\m=#1\advance\m by 1
\n=1
\p=1
\loop\ifnum\n<\m \multiply\p by \n \advance\n by 1 \repeat\number\p}}
\def\printfactorials#1{\m=#1\advance\m by 1
\n=0
\loop\ifnum\n<\m \hfil\break\number\n! = \factorial{\n} \advance\n by 1 \repeat}
\printfactorials{12}
\bye
Example for versions Baltie 3
This example uses iterative factorial definition. While loop takes a condition as parameter in round brackets. Variable out contains the output of the example. The only tricky thing is outputting multi-line variable: to do this, one had to move the sprite to the top of the screen, so that the output isn’t truncated by the lower side of the screen. 13! overflows.
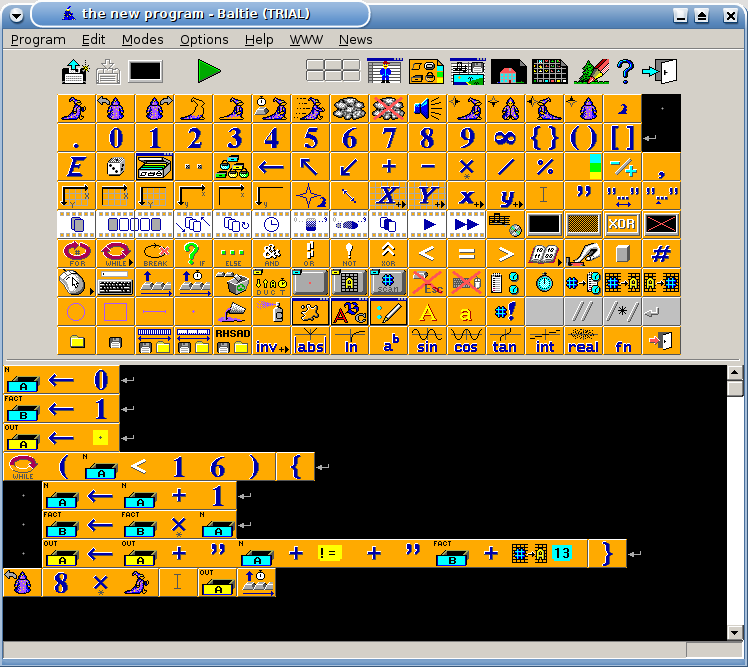
Factorial in Baltie 3
Factorial in Baltie 3 (result)
Example for versions Io-2008-01-07
This example uses iterative factorial definition. Program output for large numbers looks in the following way:
12! = 479001600
13! = 6.227021e+009
14! = 8.717829e+010
15! = 1.307674e+012
16! = 2.092279e+013
F := 1;
for(N,0,16,
N print;
"! = " print;
F println;
F := F * (N+1);
);
Example for versions Online Cat 1.3
This example uses recursive factorial definition, and works in a similar way to Fibonacci numbers example.
define fact {
dup 1 <=
[pop 1]
[dup 1 - fact *]
if
}
0
[dup write "! = " write dup fact writeln inc]
[dup 16 lteq]
while
Example for versions 64-bit BCPL Cintcode System (1 Nov 2006)
This example uses recursive factorial definition. Calculating 15! and larger results in math overflow, thus the result ends like this:
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 18000
16! = 000
GET "libhdr"
LET start() = VALOF
{ FOR i = 0 TO 16 DO writef("%n! = %n*n", i, factorial(i))
RESULTIS 0
}
AND factorial(n) = n=0 -> 1, n*factorial(n-1)
Example for versions Acme-Chef-1.01
This example uses iterative factorial definition. Ingredients measured in ml are liquid (characters), the ones measured in g are dry (numbers).
The program consists of two loops. First one, chop ... until choped, calculates the factorials in ascending order and pushes elements to be printed in the first bowl, characters and numbers alike. Smaller values which should be printed first end up at the bottom of the stack. This is cured by using the second bowl and the second loop, mash ... until mashed, which moves elements from the first bowl to the second one, so that they get to be printed in correct order.
Unfortunately, the current version of the interpreter processes liquid ingredients in a wrong way — neither liquid units of measurement, nor the command luquify modify their state, so they are printed as dry. Thus, the program output looks as follows:
0 33 32 61 32 1 10 1 33 32 61 32 1 10 2 33 32 61 32 2 10 3 33 32 61 32 6 10 4 33 32 61 32 24 10 5 33 32 61 32 120 10 6 33 32 61 32 720 10 7 33 32 61 32 5040 10 8 33 32 61 32 40320 10 9 33 32 61 32 362880 10 10 33 32 61 32 3628800 10 11 33 32 61 32 39916800 10 12 33 32 61 32 479001600 10 13 33 32 61 32 6227020800 10 14 33 32 61 32 87178291200 10 15 33 32 61 32 1307674368000 10 16 33 32 61 32 20922789888000 10
Factorial as a Piece of Cake.
This recipe calculates and prints factorials of first integers.
Ingredients.
33 ml exclamation
32 ml space
61 ml equal
10 ml newline
0 g n
1 g f
1 g one
17 g iterator
119 g second iterator
Method.
Liquify exclamation.
Liquify space.
Liquify equal.
Liquify newline.
Chop iterator.
Put n into 1st mixing bowl.
Put exclamation into 1st mixing bowl.
Put space into 1st mixing bowl.
Put equal into 1st mixing bowl.
Put space into 1st mixing bowl.
Put f into 1st mixing bowl.
Put newline into 1st mixing bowl.
Put n into 1st mixing bowl.
Add one into 1st mixing bowl.
Fold n into 1st mixing bowl.
Put f into 1st mixing bowl.
Combine n into 1st mixing bowl.
Fold f into 1st mixing bowl.
Chop iterator until choped.
Mash second iterator.
Fold n into 1st mixing bowl.
Put n into 2nd mixing bowl.
Mash second iterator until mashed.
Pour contents of 2nd mixing bowl into the baking dish.
Serves 1.
Example for versions OpenCOBOL 1.0, TinyCOBOL 0.65.9
This example uses iterative factorial definition. Variable which stores factorial value has type 9(15), i.e., a number of 15 digits. Command MULTIPLY multiplies first argument by second and (counter-intuitively) puts the result into the second argument. Command DISPLAY puts a newline after the printed value, so one has to concatenate the parts of the string before printing them. Numerical values have to be cast to string by saving them into string-type variables. There is an exception handler at multiplication, though this is optional.
Program output depends on the compiler: the number are always printed fixed-width, padded with zeros — in TinyCOBOL to total width of 18 characters, in OpenCOBOL — 15.
IDENTIFICATION DIVISION.
PROGRAM-ID. SAMPLE.
DATA DIVISION.
WORKING-STORAGE SECTION.
77 fact pic 9(15) comp.
77 n pic 99.
77 i pic 99.
77 ist pic XX.
77 factst pic X(18).
PROCEDURE DIVISION.
move 16 to n
move 0 to i
move 1 to fact
perform until i greater than n
move i to ist
move fact to factst
display ist "! = " factst
add 1 to i
multiply i by fact
on size error display "value too big"
end-multiply
end-perform.
stop run.
Example for versions Pike 7.8
This example uses recursive factorial definition. Note that int data type is extended to bignum in case of overflow.
int factorial(int n)
{
return ( n<=1 ? 1 : n * factorial(n-1) );
}
void main()
{
for (int n=0; n<=16; n++)
write(n+"! = "+factorial(n)+"\n");
}
Example for versions befungee 0.2.0
This example uses iterative factorial definition.The program consists of two loops — the first one calculates numbers from 16 to 1, the second one does the actual factorial calculation.
First of all we put 16 on top of the stack (as 4*4) — this will be the maximal number which has to be processed. The first loop follows, executed in clockwise order. One iteration puts into the stack a number which equals the previous one decremented. When this number becomes zero, loop breaks (_ in the second line), and the instruction pointer goes right.
Next the top element of the stack (0) is removed and 1 is placed there instead (this is the current factorial value). The second loop follows, executed in counter-clockwise order. One iteration performs the following actions:
-
\— two top elements of the stack (the factorial calculated earlier and the next number) are swapped (the next number becomes the topmost). If the stack contains only one element, 0 is pushed on top of it. -
:_— if the next number is 0 (or if the stack is empty), the loop breaks. -
.— next number is printed (its copy stays in the stack). -
block
,,,,"! = "pushes characters in the stack and prints them immediately. The string is scanned right-to-left, but the characters are printed from topmost to lower ones, so for the programmer the string looks exactly the way it will be printed. -
.:*— new factorial is calculated and printed (its copy stays in the stack). -
,*25— newline printed.
44* >:1-:v v ,*25 .:* ,,,,"! = ".:_ @
^ _ $1 > \: ^
Example for versions Objeck 2.0.3
This example uses built-in Factorial() function.
bundle Default {
class Factorial {
function : Main(args : String[]) ~ Nil {
for (i := 0; i <= 16; i += 1;) {
i->Print();
"! = "->Print();
i->Factorial()->PrintLine();
};
}
}
}
Example for versions Morphett's FALSE, Wouter's FALSE 1.2.CF
This example uses iterative method of factorial calculation. Variables i and f store current number (loop counter) and current factorial value. After the variables are initialized, the loop starts. [i;17=~] defines the continuation condition: as long as i doesn’t equal 17. Loop body follows: i and a string constant are printed, i is incremented, old value of f is printed and new value of f is calculated.
For Wouter’s FALSE 1.2.CF factorial values for 13 and above are calculated with overflow error.
0i: 1f:
[i;17=~]
[i; $."! = " 1+$i: f;$.10, *f:]
#
Example for versions Lingua::Shakespeare 1.00
This example uses iterative factorial definition. In scene I variables are initialized (except for loop index which is 0 by default), scene II is the loop which prints the current number, characters and the factorial, and then checks whether the current number is 17 — if it is, the loop breaks.
use Lingua::Shakespeare;
Elizabethan Factorial.
Ferdinand, for factorial.
Isabella, for loop index.
Emilia, for exclamation mark.
Sebastian, for space.
Egeus, for equality sign.
Lucio, for newline.
Act I: Factorial calculations.
Scene I: Initialization.
[Enter Isabella and Sebastian]
Isabella:
You are as fat as the product of a big black furry old cat and a white cow!
[Exit Sebastian]
[Enter Emilia]
Isabella:
You are as distasteful as the sum of Sebastian and a chihuahua!
[Exit Emilia]
[Enter Egeus]
Isabella:
You are as good as the difference between the sum of Sebastian and Emilia and a bold brave hero!
[Exit Egeus]
[Enter Lucio]
Isabella:
You are as cute as the sum of a peaceful warm delicious summer's day and a cute squirrel!
[Exit Lucio]
[Enter Ferdinand]
Isabella:
You brother!
Scene II: Loop.
Ferdinand:
Open your heart!
[Exit Ferdinand]
[Enter Emilia]
Isabella:
Speak your mind!
[Exit Emilia]
[Enter Sebastian]
Isabella:
Speak your mind!
[Exit Sebastian]
[Enter Egeus]
Isabella:
Speak your mind!
[Exit Egeus]
[Enter Sebastian]
Isabella:
Speak your mind!
[Exit Sebastian]
[Enter Ferdinand]
Isabella:
Open your heart!
[Exit Ferdinand]
[Enter Lucio]
Isabella:
Speak your mind!
[Exit Lucio]
[Enter Ferdinand]
Ferdinand:
You are as good as the sum of yourself and a rose.
Isabella:
You are as gentle as the product of myself and yourself.
Am I not as beautiful as the sum of your sweet charming lovely noble sister and a flower?
Ferdinand:
If so, let us return to scene II.
[Exeunt]
Example for versions SML/NJ 110
This example shows the naive way to implement the factorial function. However, it is not tail recursive, since the recursive function call is not the only statement on the line. The ^ operator concatenates strings. The print function prints strings. The Int.toString function converts integers into strings.
fun factorial n =
if n <= 1 then
1
else
factorial (n-1) * n;
fun aux n =
if n > 16 then
()
else (
print (Int.toString n ^ "! = " ^ Int.toString (factorial n) ^ "\n");
aux (n + 1)
);
aux 0;
Example for versions npiet 1.2
This example was generated automatically. The original program translated into the image follows; it uses iterative factorial calculation. Note that values of 13! and larger are wrong due to overflow.
main()
{
f = 1;
for ( i = 0; i <= 16; i++ )
{
__outn(i);
asm{ @"! = " }
__outn(f);
__out(10);
f = f * (i+1);
}
}

Factorial in Piet (autogenerated)

Factorial in Piet (autogenerated, 4x scale)
Example for versions Python 2.5.2, Python 2.6.5
This example uses iterative method of calculating factorials.
def factorial(n):
if n == 0:
return 1
f = 1
for i in range(1, n + 1):
f *= i
return f
for n in range(16 + 1):
print "%d! = %d" % (n, factorial(n))
Example for versions GNU Octave 3.2.3
This example uses built-in function factorial. Note that at this scale of magnitude the results are exact, but in general case Octave is not meant for arbitrary-precision computations, so huge values of factorial will be calculated approximately.
for i = 0 : 16
printf("%d! = %d\n", i, factorial(i));
endfor
Example for versions GNU Octave 3.2.3
This example uses iterative factorial definition. Semicolons at the end of lines suppress the automated output of the calculated values (in this case of fact) in interactive mode, so that the formatted output doesn’t get littered.
fact = 1;
for i = 0 : 16
printf("%d! = %d\n", i, fact);
fact *= i+1;
endfor
Example for versions GNU Octave 3.2.3
This example uses recursive factorial definition.
function f = fact(n)
if (n <= 1)
f = 1;
else
f = n * fact(n - 1);
endif
endfunction
for i = 0 : 16
printf("%d! = %d\n", i, fact(i));
endfor
Example for versions guile 1.8.5, JScheme 7.2, MIT/GNU Scheme 7.7.9
This example uses tail-recursive factorial calculation. Note that GNU Guile and MIT/GNU Scheme print correct result, while JScheme has values of factorial starting with 13! wrong due to overflow.
(define (factorial x)
(if (< x 2)
1
(* x (factorial (- x 1)))))
(do ((i 0 (+ i 1)))
((> i 16))
(display (string-append (number->string i) "! = "))
(display (number->string (factorial i)))
(newline))
Example for versions Clojure 1.0.0, Clojure 1.1.0
This example uses recursive factorial definition. range with one argument generates a list of numbers from 0 (inclusive) to this number (exclusive). str concatenates strings. dec is decrement, equivalent to (- x 1). doseg is Clojure-style loop.
(defn factorial [x]
(if (< x 2)
1
(* x (factorial (dec x)))))
(doseq [i (range 17)]
(println (str (str i "! = ") (factorial i))))
Example for versions Clojure 1.0.0, Clojure 1.1.0
To calculate factorial of a number, one can create a range of numbers from 2 to this number and calculate the product of these numbers (function apply).
(doseq [i (range 17)]
(println (str (str i "! = ") (apply * (range 2 (inc i))))))
Example for versions Seed7 2012-01-01
This example uses built-in factorial function !n. It is defined only for integer data type, so trying to calculate 13! causes an overflow. The program output looks as follows:
0! = 1
1! = 1
2! = 2
...
11! = 39916800
12! = 479001600
13! =
*** Uncaught EXCEPTION NUMERIC_ERROR raised with
{! integer <80ba990>: <SYMBOLOBJECT> 0 }
{! (in integer <80ba990> param) } at factorial-builtin.sd7(10)
main no POSINFO
$ include "seed7_05.s7i";
const proc: main is func
local
var integer: n is 0;
begin
for n range 0 to 16 do
writeln(n <& "! = " <& !n);
end for;
end func;
Example for versions Seed7 2012-01-01
This example uses recursive factorial definition. Factorial values are stored as bigInteger, so there is no overflow.
$ include "seed7_05.s7i";
include "bigint.s7i";
const func bigInteger: factorial (in var bigInteger: n) is func
result
var bigInteger: result is 1_;
begin
if n = 0_ then
result := 1_;
else
result := n * factorial(n - 1_);
end if;
end func;
const proc: main is func
local
var integer: n is 0;
begin
for n range 0 to 16 do
write(n);
write("! = ");
write(factorial(bigInteger conv n));
writeln;
end for;
end func;
Example for versions Falcon 0.9.6.6
This example uses iterative factorial calculation.
fact = 1
for i in [0:16]
printl (i, "! = ", fact)
fact *= (i+1)
end
Example for versions Falcon 0.9.6.6
This example uses recursive factorial calculation.
function fact(n)
if n==0: return 1
return n * fact(n-1)
end
for i in [0:16]
printl (i, "! = ", fact(i))
end
Example for versions iconc 9.4
This example uses recursive factorial definition. 0 to 16 is a generator which returns all integers between 0 and 16, inclusive. every ... do allows to fetch every result returned by the generator and process it (calculate factorial and perform write).
procedure factorial (n)
if n = 0 then
return 1
else if n > 0 then
return n * factorial (n - 1)
end
procedure main ()
local i
every i := 0 to 16 do
write (i, "! = ", factorial (i))
end
Example for versions iconc 9.4
This example uses iterative factorial definition written in short form. every j *= 1 to i multiplies j by all values returned by the generator 1 to i. The expression in braces calculates factorial by multiplying j by all values between 1 and i and returns it. The outer expression calculates and prints factorials of all numbers returned by the generator 0 to 16.
procedure main ()
local i, j
every write (i := 0 to 16, "! = ", { j := 1; every j *:= 1 to i; j })
end
Example for versions Rust 0.1
This example uses recursive factorial definition. Due to uint overflow values of 13! and larger are calculated incorrectly.
use std;
import std::io;
fn factorial(x: int) -> uint {
if (x <= 1) {
ret 1u;
} else {
ret (x as uint) * factorial(x - 1);
}
}
fn main() {
let i = 0;
while i <= 16 {
io::println(#fmt("%d! = %u", i, factorial(i)));
i = i + 1;
}
}
Example for versions Ceylon M1
This example calculates factorials iteratively. variable keyword points out that the value of the variable fact is going to be changed later (exactly the opposite of Java keyword final). Integer data type allows to store values of factorial without overflow. The arguments of print are concatenated without any explicit operator, but for this the first and the last elements of the list to be concatenated have to be string literals.
void run() {
variable Integer fact := 1;
for (i in 0..16) {
print("" i "! = " fact "");
fact *= i + 1;
}
}
Example for versions Factor 0.94
The first line lists the necessary dictionaries: formatting (printf), kernel (dup), math (arithmetical operators) and sequences (iota).
Next the definition of factorial word follows which replaces an integer n with its factorial on the top of the stack. To do this, it constructs an array of numbers from 0 to n — 1 (word iota) and folds it with 1 using quotation [ 1 + * ] (increment and multiply) and combinator reduce.
The main program constructs a list of numbers from 0 to 16 (iota again) and for each of them (combinator each) applies the quotation which calculates the factorial and outputs the result in required format.
Standard dictionary math.combinatorics contains word factorial defined exactly like this.
USING: formatting kernel math sequences ;
IN: factorial-example
: factorial ( n -- n! )
iota 1 [ 1 + * ] reduce ;
17 iota
[ dup factorial "%d! = %d\n" printf ] each
Example for versions Factor 0.94
This example uses a purely recursive approach to factorial calculation. Word factorial replaces n with n! on the stack with a side effect: it prints all values of factorial from 0 to n. After if combinator is applied, the stack holds values of n and n!. Words swap and over replace them with n!, n and n!; two latter values are used for printing, and the first one stays on the stack as a return value.
In the main part of the program we need to add drop to remove 16! from the stack, so that the effect of the program on the stack is ( -- ).
USING: formatting kernel math ;
IN: factorial-example
: factorial ( n -- n! )
dup
0 =
[ 1 ]
[ dup dup 1 - factorial * ]
if
swap over "%d! = %d\n" printf ;
16 factorial
drop
Example for versions Factor 0.94
This example uses a built-in word factorial defined in dictionary math.combinatorics.
USING: formatting kernel math.combinatorics sequences ;
17 iota [ dup factorial "%d! = %d\n" printf ] each
Example for versions loljs 1.1
This example uses iterative factorial definition.
HAI
I HAS A N ITZ 0
I HAS A FACTORIAL ITZ 1
IM IN YR LOOP UPPIN YR N WILE N SMALLR THAN 17
VISIBLE SMOOSH N "! = " FACTORIAL
FACTORIAL R PRODUKT OF FACTORIAL AN SUM OF N AN 1
IM OUTTA YR LOOP
KTHXBYE
Example for versions loljs 1.1
This example uses recursive factorial calculation.
HAI
HOW DUZ I FACTORIAL N
BOTH SAEM 0 AN N
O RLY?
YA RLY
FOUND YR 1
NO WAI
FOUND YR PRODUKT OF N AN FACTORIAL DIFF OF N AN 1
OIC
IF U SAY SO
I HAS A N ITZ 0
IM IN YR LOOP UPPIN YR N WILE N SMALLR THAN 17
VISIBLE SMOOSH N "! = " FACTORIAL N
IM OUTTA YR LOOP
KTHXBYE
Example for versions Mathics 0.5, Wolfram Mathematica 8.0.4
This example uses built-in factorial function !.
Do is one of the ways to run a loop — it evaluates its first argument for a sequence of numbers defined by the second argument. In this case it’s all values of i from 0 to 16, inclusive, with step of 1.
Do[Print[i, "! = ", i!] , {i, 0, 16, 1}]
Example for versions Wolfram Mathematica 8.0.4
This example uses recursive factorial definition. The first line defines Fact function. Note that the names of function arguments must have an underscore _ appended to them.
Fact[n_] := If[n == 0, 1, Fact[n - 1]*n];
For[i = 0, i <= 16, i++, Print[i, "! = ", Fact[i]]];
Example for versions CPL
(Example from language description) This is a recursive factorial definition (note the rec modifier which stresses this). To implement different processing scenarios for different values of x, a conditional expression is used instead of if.
rec function Fact1[x] = (x = 0) → 1, xFact1[x — 1]
Example for versions CPL
(Example from language description) This code shows an iterative way to calculate factorial.
result of clause allows to use a block as an expression. The body of the block must contain an assignment to variable result. The block may contain local variables, but nothing which could result in a side effect (for example, changing the values of external variables is prohibited). This clause is typically used with function definitions.
Loop body uses simultaneous assignment of new values to the variables. Both of them use small names, so the language allows to skip multiplication sign between them — xf is treated same as x*f.
function Fact2[x] = result of
§ real f = 1
until x = 0 do
f, x := xf, x — 1
result : = f §
Example for versions PostgreSQL 9.1
The task of factorials calculation is solved using standard methods only: a built-in factorial function ! (postfix form; there is also a prefix form !!) and a set function generate_series which generates a set of rows containing values between the first and the second parameters.
select n || '! = ' || (n!)
from generate_series(0,16) as seq(n);
Example for versions Dyalog APL 13.1
The first line sets the index of the first element in the lists (in this case 0). The second line sets precision when printing numbers (must be greater than the length of the largest factorial).
The third line, if read in right-to-left direction, performs the following operations:
⍳17generates a list of 17 indices, starting with 0, i.e. 0 … 16.17 / ⊂'!='generates a list of 17 strings!=.⊂isencloseoperator which allows to manipulate strings as scalars instead of character arrays./is replication operator.!⍳17applies built-in monadic function!(factorial) to each element of the list.,is a dyadic operation which concatenates left and right arguments. After two concatenations the expression evaluates to0 1 2 3 4 ... 15 16 != != ... != 1 1 2 6 24 120 720 5040 40320 362880 ..., i.e. the list of numbers followed by the list of strings and the list of factorials.3 17⍴reshapes the list into a 3x17 matrix:┌→─┬──┬──┬──┬──┬───┬───┬────┬─────┬──────┬───────┬────────┬─────────┬──────────┬───────────┬─────────────┬──────────────┐ ↓0 │1 │2 │3 │4 │5 │6 │7 │8 │9 │10 │11 │12 │13 │14 │15 │16 │ ├~─┼~─┼~─┼~─┼~─┼~──┼~──┼~───┼~────┼~─────┼~──────┼~───────┼~────────┼~─────────┼~──────────┼~────────────┼~─────────────┤ │!=│!=│!=│!=│!=│!= │!= │!= │!= │!= │!= │!= │!= │!= │!= │!= │!= │ ├─→┼─→┼─→┼─→┼─→┼──→┼──→┼───→┼────→┼─────→┼──────→┼───────→┼────────→┼─────────→┼──────────→┼────────────→┼─────────────→┤ │1 │1 │2 │6 │24│120│720│5040│40320│362880│3628800│39916800│479001600│6227020800│87178291200│1307674368000│20922789888000│ └~─┴~─┴~─┴~─┴~─┴~──┴~──┴~───┴~────┴~─────┴~──────┴~───────┴~────────┴~─────────┴~──────────┴~────────────┴~─────────────┘finally,
⍉transposes this matrix so that each row has three elements — a number, a separator string and a factorial.
The program output looks like this:
┌→─┬──┬──────────────┐
↓0 │!=│1 │
├~─┼─→┼~─────────────┤
│1 │!=│1 │
├~─┼─→┼~─────────────┤
│2 │!=│2 │
├~─┼─→┼~─────────────┤
[...25 lines of output ...]
├~─┼─→┼~─────────────┤
│16│!=│20922789888000│
└~─┴─→┴~─────────────┘
The matrix is displayed as a table with cell borders drawn, because it contains boxed strings.
⎕IO←0
⎕PP←18
⍉3 17⍴ (⍳17) , (17 / ⊂'!=') , !⍳17
Example for versions Baltie 3
A shorter program to calculate factorials, provided by Bohumír Soukup of SGP systems. It prints the factorials directly to output stream without storing them in temporary variable.
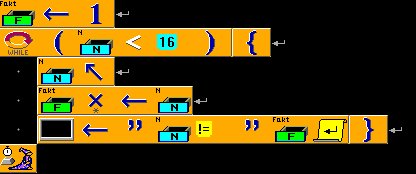
Factorial in Baltie 3 (shorter version)
Example for versions Dyalog APL 13.1
This example calculates factorial of a number N by applying multiplication reduction to a list of numbers from 1 to N, inclusive (expression ×/1+⍳). The anonymous D-function applies this expression to its right argument and concatenates the result with the argument itself and a string separator. Note that in this case the string is not boxed. The function, in turn, is applied to a list of numbers from 0 to 16, written in a column, i.e. as a two-dimensional 17x1 array. Program output looks like this:
┌→───────────────────┐
↓0 != 1 │
├+──────────────────→┤
│1 != 1 │
├+──────────────────→┤
│2 != 2 │
├+──────────────────→┤
[...25 lines of output ...]
├+──────────────────→┤
│16 != 20922789888000│
└+──────────────────→┘
⎕IO←0
⎕PP←18
{⍵, '!=', ×/1+⍳⍵}¨17 1⍴⍳17
Example for versions Nimrod 0.8.8
This example uses recursive factorial definition.
proc factorial(n: int): int64 =
if n == 0:
result = 1
else:
result = n * factorial(n - 1)
for i in countup(0,16):
echo i, "! = ", factorial(i)
Example for versions Nimrod 0.8.8
This example uses iterative factorial calculation. Note that you can’t just omit int64 in variable definition, since its type will be deduced as integer, and it will overflow on 13!.
var f: int64 = 1
for i in countup(0,16):
echo i, "! = ", f
f = f * (i + 1)
Example for versions bwBASIC 2.50
Factorials are calculated iteratively. Note the type inference: data type for storing factorial values is not declared explicitly, and yet the larger values are calculated without an overflow error.
f = 1
FOR i = 0 TO 16
PRINT i; "! ="; f
f = f * (i + 1)
NEXT i
Example for versions VBScript 5.7, VBScript 5.8
This example shows iterative factorial calculation. Note that no overflow happens, though the type of factorial variable is inferred from its usage and never set explicitly.
f = 1
For i = 0 To 16
WScript.Echo(i & "! = " & f)
f = f * (i + 1)
Next
Example for versions Wirth's PL/0 (1976)
The language makes it impossible to print any characters, so the program just outputs the pairs number-factorial without any separators. Running this program results in the following output:
0 var n, f;
1 begin
2 n := 0;
4 f := 1;
6 while n # 16 do
10 begin
10 n := n + 1;
14 f := f * n;
18 end;
19 end.
0 jmp 1 1
1 int 1 5
2 lit 1 0
3 sto 1 3
4 lit 1 1
5 sto 1 4
6 lod 1 3
7 lit 1 16
8 opr 1 9
9 jpc 1 19
10 lod 1 3
11 lit 1 1
12 opr 1 2
13 sto 1 3
14 lod 1 4
15 lod 1 3
16 opr 1 4
17 sto 1 4
18 jmp 1 6
19 opr 1 0
start pl/0
0
1
1
1
2
2
3
6
4
24
5
120
6
720
7
5040
8
40320
9
362880
10
3628800
11
39916800
12
479001600
13
1932053504
14
1278945280
15
2004310016
16
2004189184
end pl/0
var n, f;
begin
n := 0;
f := 1;
while n # 16 do
begin
n := n + 1;
f := f * n;
end;
end.
Example for versions A++ Interpreter
The first expression loads init library which contains all main language constructs (loops, conditional jumps, comparisons etc.). All of them are not included in language core but instead are defined via a limited set of primitives; thus, for example, if construct is defined as follows::
(define true (lambda (x y)
x))
(define false (lambda (x y)
y))
(define if (lambda (b t f)
(b t f)))
The second example defines factorial as a recursive function. Note that the language standard defines two kinds of numbers — regular integers with typical arithmetical operations on them and “nominal” zero, one, two, ..., ten with specific operations. Numbers of different types can’t be decoded one into another and are to be used separately; in this case we use regular integers.
The third expression is the main loop, and the fourth one just calls it. print command ends the output with line feed, so overall program output looks as follows:
-->0
-->! =
-->1
-->1
-->! =
-->1
-->2
-->! =
-->2
-->3
-->! =
-->6
-->4
-->! =
-->24
-->5
-->! =
-->120
...
Factorial values are calculated correctly up to 12!, after that they overflow and are printed as -1.
(load "app/init.app")
(define factorial (lambda(n)
(if (equal n 0)
1
(* n (factorial (- n 1))))))
(define main
(lambda(n)
(while (not (equal n 17))
(lambda()
(print n)
(print "! = ")
(print (factorial n))
(define n (+ n 1))))))
(main 0)
Example for versions E-on-Java 0.9.3
E is implicitly-typed language; :int in function signature is not a type declaration but rather a “guard” — a contract which guarantees that factorial function will be given only integer arguments and it will return only integer values. Such limitations are not necessary but quite useful for code auditing.
def factorial(n :int) :int {
if (n == 0) {
return 1
} else {
return n * factorial(n-1)
}
}
for n in 0..16 {
println(n.toString(10) + "! = " + factorial(n).toString(10))
}
Example for versions GAP 4.4.12
This example uses standard Factorial function.
for n in [0..16] do
Print(n, "! = ", Factorial(n), "\n");
od;
Example for versions Dart 1.1.1
This example uses recursive factorial definition. int datatype is an integer of arbitrary size.
int factorial(int n) => n == 0 ? 1 : n * factorial(n - 1);
main() {
for (int i = 0; i <= 16; ++i) {
print('$i! = ${factorial(i)}');
}
}
Example for versions Dart 1.1.1
This example uses iterative factorial definition.
main() {
int fact = 1;
for (int i = 0; i <= 16; ++i, fact *= i) {
print('$i! = $fact');
}
}
Example for versions Picat 0.7
This example implements recursive factorial definition using a predicate.
factorial(0, F) => F = 1.
factorial(N, F), N > 0 => factorial(N - 1, F1), F = N * F1.
main =>
foreach (I in 0 .. 16)
factorial(I, F),
writef("%w! = %w\n", I, F)
end.
Example for versions Picat 0.7
This example implements recursive factorial definition using a function.
factorial(0) = 1.
factorial(N) = F, N > 0 => F = N * factorial(N - 1).
main =>
foreach (I in 0 .. 16)
writef("%w! = %w\n", I, factorial(I))
end.
Example for versions Snap! 4.0
This example shows iterative calculation of factorial. To output results in required multiline format a global list variable is used.
Factorial (iterative) example in Snap!
Example for versions Snap! 4.0
This example uses recursive method of factorial calculation. Snap! allows to create user-defined blocks, in this case factorial block of type reporter (a block that returns a value, i.e. a function block). The newly defined block appears in the blocks palette immediately, and can be used when editing its own definition, thus allowing recursive calls.
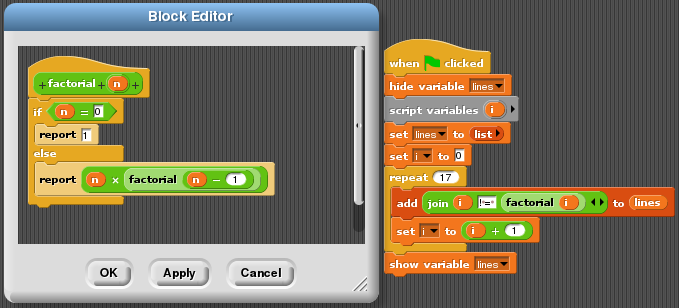
Factorial (recursive) in Snap!
Example for versions Windows PowerShell 5.0
function Get-Factorial ($n) {
if ($n -eq 0) {
return 1
}
$fact = 1
1..$n | ForEach { $fact *= $_ }
return $fact
}
foreach ($i in 0..16) {
echo ("{0}! = {1}" -f $i,(Get-Factorial $i))
}
Example for versions W 0.0.1
Repeat 15
[
Item x = 1
Repeat #
[
x = x * #
]
Type(x)
]