Quadratic equation
A quadratic equation is an equation of form Ax2 + Bx + C = 0, where A, B and C are given constants (with a constraint A != 0).
To solve it, a discriminant is calculated: D = B2-4AC. If D = 0, the equation has one real root x = -B/2A, otherwise it has two roots x1 = (-B+sqrt(D))/2A, x2 = (-B-sqrt(D))/2A (the roots are real or complex, depending on whether D is positive or negative).
The task is to read integer constants A, B and C entered by user, calculate the roots of the equation and output them. If A = 0, output an error message “Not a quadratic equation”. Output real roots as a single double, and complex roots a + ib as (a,b).
This class of examples shows processing of floating-point and complex numbers (if the language provides these data types). Besides, both console and graphical user interface can be used for interacting with the user.
Example for versions Borland C++ Builder 6, Microsoft Visual C++ 9 (2008)
This example uses a template class complex<>, provided in STL. All calculations are done in complex numbers, because this allows not to worry about the sign of discriminant and representation of the roots.
Operator >> of complex is overloaded so that it can recognize several formats of the number, so the input constants are read not as integers but as complex numbers without imaginary part. This implementation allows to solve quadratic equations not only with integer coefficients but also with floating-point and even complex ones.
Operator << is also overloaded to print the number x as (x.real(),x.imag()), so to print roots without imaginary part as a single double, function print was created.
#include <iostream>
#include <complex>
#include <cmath>
using namespace std;
void print(int ind, complex<double> x)
{ cout << "x" << ind << " = ";
if (abs(x.imag()) < 1E-6)
cout << x.real() << endl;
else cout << x << endl;
}
int main()
{ complex<double> A, B, C, D;
cout << "A = ";
cin >> A;
if (abs(A)<1E-3)
{ cout << "Not a quadratic equation" << endl;
return 1;
}
cout << "B = ";
cin >> B;
cout << "C = ";
cin >> C;
A *= 2;
D = B*B-A*C*2.0;
if (abs(D)<1E-3)
cout << "x = " << (-B/A).real();
else
{ print(1, (-B+sqrt(D))/A);
print(2, (-B-sqrt(D))/A);
}
return 0;
}
Example for versions Algol68g-1.18.0
A direct translation of the C++ example.
PROC print root = (INT ind, LONG COMPL x)VOID:
( print(("x", ind, " := "));
IF ABS(im OF x) < 1E-6 THEN
print((re OF x, new line))
ELSE print((x, new line))
FI
);
main:
( LONG COMPL a, b, c, d, x1, x2;
print(("a := "));
read((a));
IF ABS a <1E-3 THEN
print(( "Not a quadratic equation", new line));
stop
FI;
print(("b := "));
read((b));
print(("c := "));
read((c));
a *:= 2;
d := b*b-a*c*2.0;
IF ABS d <1E-3 THEN
print(("x := ", re OF (-b/a)))
ELSE
print root(1, (-b+long complex sqrt(d))/a);
print root(2, (-b-long complex sqrt(d))/a)
FI
)
Example for versions SpiderMonkey 1.7
The example is meant to be executed from the web-browser. To run the example, copy the code to a file quadratic.js and create an HTML file placed in the same directory and containing the following text:
<head>
<script type="text/javascript" src="quadratic.js"></script>
</head>
<body>
<form name="quadratic">
<input type="number" required="required" name="A">
<input type="number" required="required" name="B">
<input type="number" required="required" name="C">
<input type="button" value="Solve" onClick="solve()">
</form>
<p id="output">
</p>
</body>
This will create a web-page with three input fields and a button. The equation will be solved once the button is pressed, and the roots will be printed beneath the inputs.
JavaScript doesn’t provide complex numbers, so the calculations are done in real numbers with separate check for discriminant sign. This implementation allows to solve quadratic equations not only with integer coefficients but also with floating-point ones.
function print(real, imag)
{ if (Math.abs(imag)<1E-6)
return real;
else
return '('+real+','+imag+')';
}
function solve()
{ A = document.quadratic.A.value;
if (Math.abs(A)<1E-3)
{ document.getElementById('output').innerHTML = 'Not a quadratic equation';
return;
}
B = document.quadratic.B.value;
C = document.quadratic.C.value;
A = 2*A;
D = B*B-2*A*C;
if (Math.abs(D)<1E-3)
{ document.getElementById('output').innerHTML = 'x = '+(-B/A);
return;
}
if (D>0)
document.getElementById('output').innerHTML = 'x1 = '+print((-B+Math.sqrt(D))/A, 0)+'<br />x2 = '+print((-B-Math.sqrt(D))/A, 0);
else
document.getElementById('output').innerHTML = 'x1 = '+print(-B/A,Math.sqrt(-D)/A)+'<br />x2 = '+print(-B/A,-Math.sqrt(-D)/A);
}
Example for versions Sanscript 2.2
Sanscript is a fully visual programming language, so no source code is available. See screeshots instead.
This example contains a lot of branches on condition, and in Sanscript each branch is described in a new flowgram.
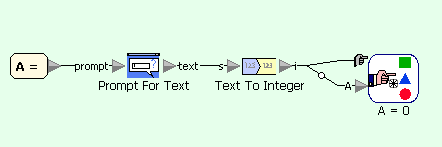
Quadratic equation example in Sanscript (main flowgram)
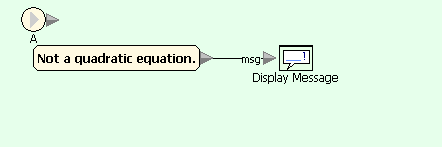
Quadratic equation example in Sanscript (on condition A=0)
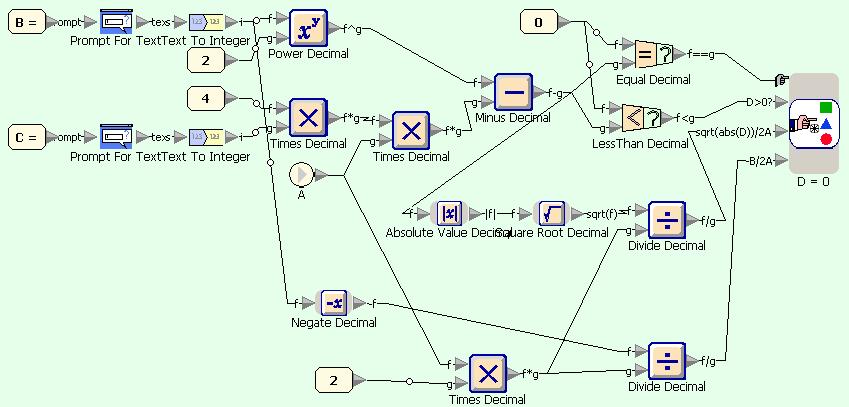
Quadratic equation example in Sanscript (on condition A=default)
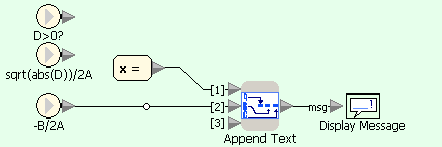
Quadratic equation example in Sanscript (on condition D=0)
Quadratic equation example in Sanscript (on condition D=default)
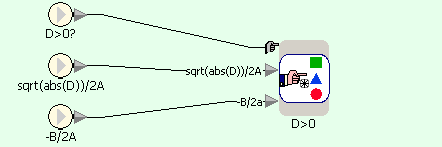
Quadratic equation example in Sanscript (on condition D>0)
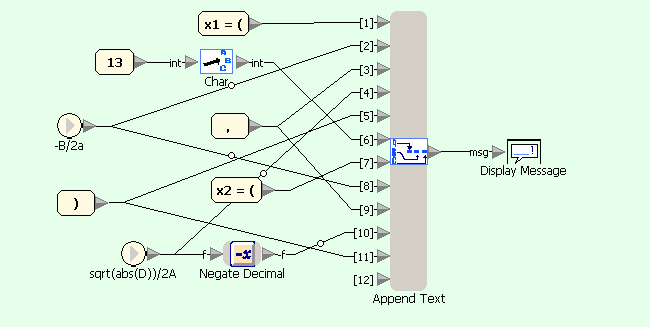
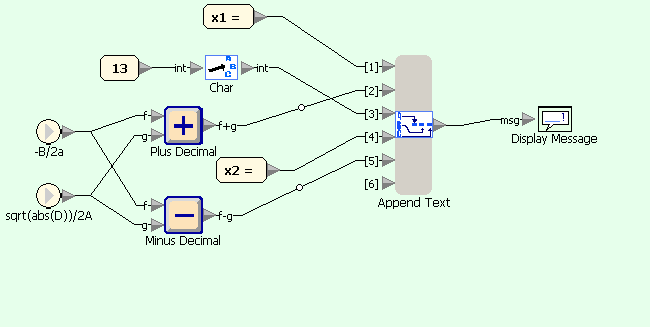
Quadratic equation example in Sanscript (on condition D<0)
Example for versions gcj 3.4.5, Groovy 1.7, Sun Java 6
Java doesn’t provide complex numbers, so the calculations are done in real numbers with separate check for discriminant sign. This implementation allows to solve quadratic equations not only with integer coefficients but also with floating-point ones.
The coefficients are read from stream System.in, which allows only individual bytes to be read directly, so two wrapper classes InputStreamReader and BufferedReader are used to make reading more comfortable. The strings read from System.in are converted into double values using parseDouble method of class Double. In Java all input operations must be wrapped in try ... catch blocks to handle IOException — class of exceptions which are thrown by reading routines.
import java.util.*;
import java.io.*;
public class Quadratic {
static String print(double real, double imag)
{ if (Math.abs(imag)<1E-6)
return ""+real;
else
return "("+real+","+imag+")";
}
public static void main(String[] args)
{ double A,B,C,D;
try {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
System.out.print("A = ");
A = Double.parseDouble(br.readLine());
if (Math.abs(A)<1E-3)
{ System.out.println("Not a quadratic equation.");
return;
}
System.out.print("B = ");
B = Double.parseDouble(br.readLine());
System.out.print("C = ");
C = Double.parseDouble(br.readLine());
}
catch (Exception e) {
System.err.println("An error occured while reading input parameters.");
return;
}
A = 2*A;
D = B*B-2*A*C;
if (Math.abs(D)<1E-3)
{ System.out.println("x = "+(-B/A));
return;
}
if (D>0)
System.out.println("x1 = "+print((-B+Math.sqrt(D))/A, 0)+"\nx2 = "+print((-B-Math.sqrt(D))/A, 0));
else
System.out.println("x1 = "+print(-B/A,Math.sqrt(-D)/A)+"\nx2 = "+print(-B/A,-Math.sqrt(-D)/A));
}
}
Example for versions Oracle 10g SQL, Oracle 11g SQL
This example was tested in SQL*Plus and TOAD.
Pure SQL allows to input values at runtime in the form of substitution variables. To define a substitution variable, use its name (in this case A, B and C) with an ampersand & before it each time you need to reference it. When the query needs to be executed, you will receive a prompt to enter the values of the variables. Each reference to such variable will be replaced with its value, and the resulting query will be executed.
There are several ways to input the values for substitution variables. In this example first reference to each variable has double ampersand && before its name. This way the value of the variable has to be entered only once, and all following references will be replaced with the same value (using single ampersand in SQL*Plus asks to enter the value for each reference to the same variable). PL/SQL Developer requires that all variables have single & before their names, otherwise ORA-01008 “Not all variables bound” exception will be raised.
Note that the references are substituted with the values “as is”, so negative values of coefficients have to be entered in brackets.
First line of the example sets the character for decimal separator which is used when the numbers are converted into strings.
The query itself is composed of four different queries. Each query returns a string containing the result of calculations for one case of quadratic equation, and returns nothing for three other cases. The results of each query are united to produce the final result.
alter session set NLS_NUMERIC_CHARACTERS='. ';
select 'Not a quadratic equation.' ans
from dual
where &&A = 0
union
select 'x = ' || to_char(-&&B/2/&A)
from dual
where &A != 0 and &B*&B-4*&A*&&C = 0
union
select 'x1 = ' || to_char((-&B+sqrt(&B*&B-4*&A*&C))/2/&A) || ', x2 = ' || to_char(-&B-sqrt(&B*&B-4*&A*&C))/2/&A
from dual
where &A != 0 and &B*&B-4*&A*&C > 0
union
select 'x1 = (' || to_char(-&B/2/&A) || ',' || to_char(sqrt(-&B*&B+4*&A*&C)/2/&A) || '), ' ||
'x2 = (' || to_char(-&B/2/&A) || ',' || to_char(-sqrt(-&B*&B+4*&A*&C)/2/&A) || ')'
from dual
where &A != 0 and &B*&B-4*&A*&C < 0;
Example for versions clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
Common Lisp provides complex numbers as datatype, printed as #C(real imag). write-to-string converts a number into a string.
Note that for interactive evaluation it’s enough to add (quadratic-roots-2 1 0 1) to see the result of calculation, while for compiled execution you’ll have to wrap call of this function in printing command, like (format t (quadratic-roots-2 1 0 1)).
(defun quadratic-roots-2 (A B C)
(cond ((= A 0) (string "Not a quadratic equation."))
(t
(let ((D (- (* B B) (* 4 A C))))
(cond ((= D 0) (concatenate 'string "x = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A)))))
(t
(values (concatenate 'string "x1 = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A))))
(concatenate 'string "x2 = " (write-to-string (/ (- (- B) (sqrt D)) (* 2 A)))))))))))
Example for versions gnat 3.4.5, gnat 4.3.2
Ada provides complex datatype, which requires using packages Generic_Complex_Types and Generic_Complex_Elementary_Functions and instantiating them with the type of complex number to use (in this case — floating-point numbers). Ada doesn’t support implicit data type conversions, so all casts are done explicitly.
with Ada.Text_IO,
Ada.Integer_Text_IO,
Ada.Float_Text_IO,
Ada.Numerics.Elementary_Functions,
Ada.Text_IO.Complex_IO,
Ada.Numerics.Generic_Complex_Types,
Ada.Numerics.Generic_Complex_Elementary_Functions;
use Ada.Text_IO, Ada.Integer_Text_IO, Ada.Float_Text_IO;
procedure QuadraticEquation is
package Complex_Types is new Ada.Numerics.Generic_Complex_Types (Float);
package Complex_Functions is new Ada.Numerics.Generic_Complex_Elementary_Functions(Complex_Types);
package Complex_IO is new Ada.Text_IO.Complex_IO (Complex_Types);
use Complex_Types, Complex_Functions, Complex_IO;
A,B,C,D: Integer;
A2f, Bf, S: Float;
Dc: Complex;
begin
Put("A = ");
Get(Item => A);
if A = 0 then
Put_Line("Not a quadratic equation.");
return;
end if;
Put("B = ");
Get(B);
Put("C = ");
Get(C);
A2f := Float(2*A);
Bf := Float(B);
D := B*B-4*A*C;
if D = 0 then
Put("x = ");
Put(-Bf/A2f);
elsif D > 0 then
S := Ada.Numerics.Elementary_Functions.Sqrt(Float(D));
Put("x1 = ");
Put((-Bf+S)/A2f);
Put_Line("");
Put("x2 = ");
Put((-Bf-S)/A2f);
else
Dc := Compose_From_Cartesian (Re => Float(D), Im => 0.0);
Put("x1 = ");
Put((-Bf+Complex_Functions.Sqrt(Dc))/A2f);
Put_Line("");
Put("x2 = ");
Put((-Bf-Complex_Functions.Sqrt(Dc))/A2f);
end if;
end QuadraticEquation;
Example for versions GHC 6.10.4
Haskell provides complex datatype. Function quadratic accepts a list of complex numbers and returns a list of equation roots. Notation root sign allows to generalize the notation of roots for two signs of square root.
module Main where
import Data.Complex
import System.IO (hFlush, stdout)
quadratic :: (Complex Double, Complex Double, Complex Double) -> [Complex Double]
quadratic (0, _, _) = []
quadratic (a, b, c)
| d == 0 = [root (+)]
| otherwise = [root (+), root (-)]
where d = b*b - 4*a*c
root sign = sign (-b) (sqrt d) / (2*a)
main = do
putStr "A = "
hFlush stdout
a <- readLn :: IO Double
putStr "B = "
hFlush stdout
b <- readLn :: IO Double
putStr "C = "
hFlush stdout
c <- readLn :: IO Double
print $ quadratic (realToFrac a, realToFrac b, realToFrac c)
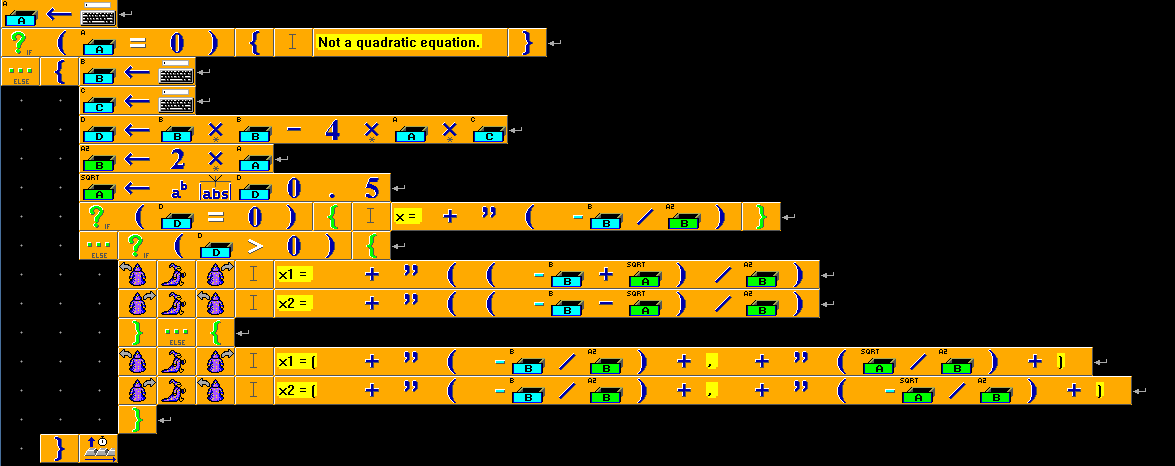
Example for versions Scratch 1.4
Scratch is a graphical language, the print-screen contains the actual information about the program, source text is only a transcription. This example features the usage of text input in Scratch, which is done with command ask "..." and wait. This command makes the sprite “say” the associated message (used as prompt) and displays an input window below the sprite. Once the information is entered, is can be accessed through predefined variable answer, which is copied to local variables before entering next values.
ask "A = ?" and wait
set A to answer
if A = 0
say "Not a quadratic equation"
else
ask "B = ?" and wait
set B to answer
ask "C = ?" and wait
set C to answer
set D to B*B + (-4)*A*C
set re to B/(-2*A)
if D = 0
say join ("x = " re)
else
set im to (sqrt of (abs of D)) / (2*A)
if D > 0
say join (join ("x1 = " (re+im)) join (", x2 = " (re-im)))
else
say join (join ("x1 = (" join (re join (", " im))) join ("), x2 = (" join (re join (", -" join (im ")")))))
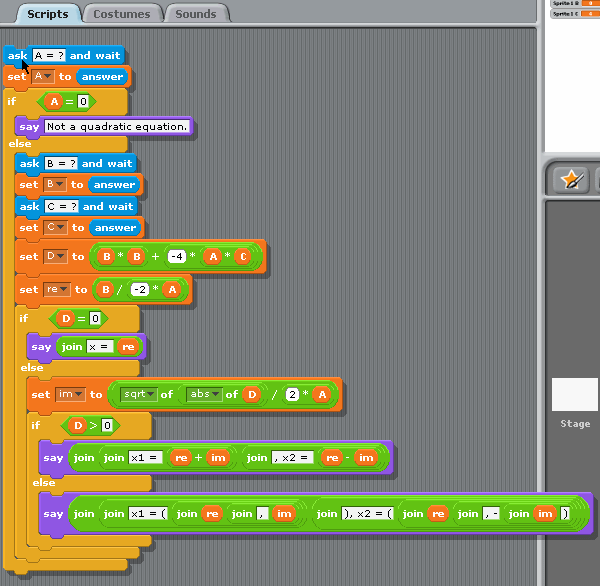
Quadratic equation example in Scratch
Example for versions UCBLogo 6.0
This example defines function quadraticwhich accepts coefficients of quadratic equation and prints the roots. Usage is quadratic 1 -2 1.
to quadratic :A :B :C
if :A = 0 [(print [Not a quadratic equation.])
stop
]
make "D :B*:B - 4*:A*:C
if :D = 0 [(print [x = ] -:B/2/:A)
stop
]
if :D > 0 [(print [x1 = ] (-:B+sqrt :D)/2/:A)
(print [x2 = ] (-:B-sqrt :D)/2/:A)
stop
]
(print [x1 = (] -:B/2/:A [,] (sqrt (-:D))/2/A [)])
(print [x2 = (] -:B/2/:A [,] (-sqrt (-:D))/2/A [)])
end
Example for versions Visual Prolog 7.2
Create a new project with UI Strategy “Console” and replace contents of files main.cl and main.pro with given code.
In main.cl the only added line q : () procedure(). specifies that q is a predicate which doesn’t accept parameters. Keyword procedure describes the behavior of predicate, indicating that is will always succeed with only one solution, so no backtracking is required.
In main.pro the actual description of newly specified predicate takes place. q takes no arguments, since it reads everything it needs from stdio. Conditional evaluation (construct if-then-else) works much like in other languages, with the difference of ! sign before then clause. This is a cut, meaning that once the condition is satisfied, no backtracking is needed.
The tricky part about this example is that we can’t calculate discriminant before checking its sign like in other examples. Default data type for D in assignment D = B*B-4*A*C is uReal, which is unsigned and can’t hold negative values. Thus, we have to check the sign of discriminant first and then assign its absolute value to a variable D.
% main.cl
class main
open core
predicates
classInfo : core::classInfo.
q : () procedure().
predicates
run : core::runnable.
end class main
% main.pro
implement main
open core
constants
className = "main".
classVersion = "".
clauses
classInfo(className, classVersion).
q() :-
stdio::write("A = "),
A = stdio::read(),
if (A = 0), ! then
stdio::write("Not a quadratic equation."), stdio::nl
else
stdio::write("B = "),
B = stdio::read(),
stdio::write("C = "),
C = stdio::read(),
if (B*B = 4*A*C), ! then
stdio::writef("x = %f", -B/2.0/A)
elseif (B*B > 4*A*C), ! then
D = B*B-4*A*C,
stdio::writef("x1 = %f\n", (-B+math::sqrt(D))/2.0/A),
stdio::writef("x2 = %f", (-B-math::sqrt(D))/2.0/A)
else
D = -B*B+4*A*C,
stdio::writef("x1 = (%f, %f)\n", -B/2.0/A, math::sqrt(D)/2.0/A),
stdio::writef("x2 = (%f, %f)", -B/2.0/A, -math::sqrt(D)/2.0/A)
end if
end if.
clauses
run():-
console::init(),
q(),
succeed().
end implement main
goal
mainExe::run(main::run).
Example for versions Free Pascal 2.0.4, Free Pascal 2.2.0, gpc 20070904, Turbo Pascal 1.0, Turbo Pascal 2.0, Turbo Pascal 3.0, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 6.0
Pascal has built-in complex data type complex, but using it is inconvenient in this case, because writeln can’t output complex numbers directly, and functions Re and Im would have to be used. In this example calculations are done in real numbers. Library function halt (added in Extended Pascal) exits current block (in later versions it is replaced with exit).
program Quadratic;
var
A,B,C,D: integer;
begin
write('A = ');
readln(A);
if (A=0) then
begin
writeln('Not a quadratic equation.');
halt;
end;
write('B = ');
readln(B);
write('C = ');
readln(C);
D := B*B-4*A*C;
if (D=0) then
begin
writeln('x = ',-B/2.0/A);
halt;
end;
if (D>0) then
begin
writeln('x1 = ',(-B+Sqrt(D))/2.0/A);
writeln('x2 = ',(-B-Sqrt(D))/2.0/A);
end
else
begin
writeln('x1 = (',-B/2.0/A,',',Sqrt(-D)/2.0/A,')');
writeln('x2 = (',-B/2.0/A,',',-Sqrt(-D)/2.0/A,')');
end;
end.
Example for versions QuickBASIC 4.5
PRINT "A = "
INPUT A
IF (A = 0) THEN
PRINT "Not a quadratic equation."
ELSE
PRINT "B = "
INPUT B
PRINT "C = "
INPUT C
D = B * B - 4 * A * C
IF (D = 0) THEN
PRINT "x = " + STR$(-B / 2! / A)
ELSE
IF (D > 0) THEN
PRINT "x1 = " + STR$((-B + SQR(D)) / 2! / A)
PRINT "x2 = " + STR$((-B - SQR(D)) / 2! / A)
ELSE
PRINT "x1 = (" + STR$(-B / 2! / A) + "," + STR$(SQR(-D) / 2! / A) + ")"
PRINT "x2 = (" + STR$(-B / 2! / A) + "," + STR$(-SQR(-D) / 2! / A) + ")"
END IF
END IF
END IF
Example for versions gmcs 2.0.1, Microsoft Visual C# 2008
using System;
class Program
{
static void Main(string[] args)
{
int A, B, C, D;
try
{ Console.Write("A = ");
A = Convert.ToInt32(Console.ReadLine());
Console.Write("B = ");
B = Convert.ToInt32(Console.ReadLine());
Console.Write("C = ");
C = Convert.ToInt32(Console.ReadLine());
}
catch
{ Console.WriteLine("Invalid input");
return;
}
if (A == 0)
{ Console.WriteLine("Not a quadratic equation.");
return;
}
D = B * B - 4 * A * C;
if (D == 0)
Console.WriteLine("x = {0}", -B / 2.0 / A);
else if (D > 0)
Console.WriteLine("x1 = {0}\nx2 = {1}", (-B + Math.Sqrt(D)) / 2 / A, (-B - Math.Sqrt(D)) / 2 / A);
else
Console.WriteLine("x1 = ({0},{1})\nx2 = ({0},-{1})", -B/2.0/A, Math.Sqrt(-D)/2/A);
}
}
Example for versions Microsoft Visual Basic .NET 9 (2008), vbnc 2.4.2
Module Module1
Sub Main()
Dim A, B, C, D As Integer
Dim p1, p2 As Double
Try
Console.Write("A = ")
A = Val(Console.ReadLine())
Console.Write("B = ")
B = Val(Console.ReadLine())
Console.Write("C = ")
C = Val(Console.ReadLine())
Catch ex As Exception
Console.WriteLine("Invalid input.")
Return
End Try
If A = 0 Then
Console.WriteLine("Not a quadratic equation.")
Return
End If
D = B * B - 4 * A * C
p1 = -B / 2.0 / A
p2 = Math.Sqrt(Math.Abs(D)) / 2.0 / A
If D = 0 Then
Console.Write("x = " & p1.ToString())
ElseIf D > 0 Then
Console.WriteLine("x1 = " & (p1 + p2).ToString())
Console.WriteLine("x2 = " & (p1 - p2).ToString())
Else
Console.WriteLine("x1 = (" & p1.ToString() & "," & p2.ToString() & ")")
Console.WriteLine("x2 = (" & p1.ToString() & ",-" & p2.ToString() & ")")
End If
End Sub
End Module
Example for versions j602
Run calc'' in an interactive J session after loading the file. The function calc2 calculates the roots of the equation using J’s built in root function(p.).
print=: 1!:2&2
read=: 3 : '". 1!:1[1'
a=: 0&{ [ b=: 1&{ [ c=: 2&{
d=: *:@b - [:*/4,a,c
roots=: ([:-b%2*a)`(+:@a %~ (,-)@%:@d + -@b)@.([:*/*)
input=: 3 : 0
A=: read'' [ print 'A = '
B=: read'' [ print 'B = '
C=: read'' [ print 'C = '
)
calc=: 3 : 0
input''
if. A=0 do. print 'Not a quadratic equation' throw. end.
rt=: roots A,B,C
disp rt
)
disp=: 3 : 0
form=: ((('('&,)@":@{.,',',(,&')')@":@}.)@+.)`":@.(=+)
if. 1<# ~.y do.
print 'x1 = ', form 0{y
print 'x2 = ', form 1{y
else.
print 'x = ', form {.y
end.
)
calc2=: 3 : 0
input''
rt=: ;}.p.|.A,B,C
disp rt
)
Example for versions Simply Scala
This example shows that string processing and Math in Scala are implemented similarly to Java.
def output(real: Double, imag: Double): String =
if (imag == 0) ""+real
else "("+real+","+imag+")"
def solve(A: Int, B: Int, C: Int)
{ if (A == 0) print("Not a quadratic equation.")
else
{ def D = B*B - 4*A*C
if (D == 0) print("x = "+output(-B/2.0/A, 0))
else if (D > 0) print("x1 = "+output((-B+Math.sqrt(D))/2.0/A, 0)+"\nx2 = "+output((-B-Math.sqrt(D))/2.0/A, 0))
else print("x1 = "+output(-B/2/A, Math.sqrt(-D)/2.0/A)+"\nx2 = "+output(-B/2/A, -Math.sqrt(-D)/2.0/A))
}
}
Example for versions gawk 3.1.6, Jawk 1.02, mawk 1.3.3
{ A = $1
B = $2
C = $3
if (A == 0)
print "Not a quadratic equation"
else
{ D = B*B-4*A*C
if (D == 0)
print "x = " (-B/2/A)
else if (D > 0)
{ print "x1 = " ((-B+sqrt(D))/2/A)
print "x2 = " ((-B-sqrt(D))/2/A)
}
else
{ print "x1 = (" (-B/2/A) "," (sqrt(-D)/2/A) ")"
print "x2 = (" (-B/2/A) "," (-sqrt(-D)/2/A) ")"
}
}
}
Example for versions Borland C++ Builder 6, g++ 3.4.5, gcc 3.4.5, gcc 3.4.5 (Objective-C), gcc 4.2.4, Microsoft Visual C++ 9 (2008), tcc 0.9.25
This example works both for C and C++, as well as for Objective-C which is superset of C.
#include <math.h>
#include <stdio.h>
int main()
{
int A, B, C;
double D;
printf("A = ");
scanf("%d", &A);
if (A == 0) {
printf("Not a quadratic equation.\n");
return 0;
}
printf("B = ");
scanf("%d", &B);
printf("C = ");
scanf("%d", &C);
D = B * B - 4 * A * C;
if (D == 0) {
printf("x = %f\n", -B / 2.0 / A);
return 0;
}
if (D > 0) {
printf("x1 = %f\nx2 = %f\n",
(-B + sqrt(D)) / 2.0 / A, (-B - sqrt(D))/ 2.0 / A);
} else {
printf("x1 = (%f, %f)\nx2 = (%f, %f)\n",
-B / 2.0 / A, sqrt(-D) / 2.0 / A, -B / 2.0 / A, -sqrt(-D) / 2.0 /A);
}
return 0;
}
Example for versions D1, D2
import std.c.stdio;
import std.stdio;
import std.math;
int main() {
int A, B, C;
writef("A = ");
scanf("%d", & A);
if (A==0)
{ writefln("Not a quadratic equation.");
return 0;
}
writef("B = ");
scanf("%d", & B);
writef("C = ");
scanf("%d", & C);
A*=2;
float D = B*B-2*A*C;
if (D == 0)
{ writefln("x = %f\n",-B*1.0/A);
return 0;
}
if (D>0)
writefln("x1 = %f\nx2 = %f",(-B+sqrt(D))/A,(-B-sqrt(D))/A);
else
writefln("x1 = (%f, %f)\nx2 = (%f, %f)",-B*1.0/A,sqrt(-D)/A,-B*1.0/A,-sqrt(-D)/A);
return 0;
}
Example for versions erl 5.7.3
fread function can return several values: eof to mark that the input stream has ended, tuple {ok, value} if the read succeeded, and tuple {error, message} if it failed for any other reason. Thus, when a number is read, it has to be extra processed to stripe it of these things.
-module(prog).
-export([main/0]).
solve(A, B, C) ->
D = B*B - 4*A*C,
if (D == 0) -> io:format("x = ~f~n", [-B*0.5/A]);
true ->
if (D > 0) ->
SQ = math:sqrt(D),
io:format("x1 = ~f~nx2 = ~f", [(-B+SQ)/2/A, (-B-SQ)/2/A]);
true -> SQ = math:sqrt(-D),
io:format("x1 = (~f,~f)~nx2 = (~f,~f)", [-0.5*B/A, 0.5*SQ/A, -0.5*B/A, -0.5*SQ/A])
end
end
.
main() ->
case io:fread("A = ", "~d") of
eof -> true;
{ok, X} ->
[A] = X,
if (A == 0) -> io:format("Not a quadratic equation.");
true ->
case io: fread("B = ", "~d") of
eof -> true;
{ok, Y} ->
[B] = Y,
case io: fread("C = ", "~d") of
eof -> true;
{ok, Z} ->
[C] = Z,
solve(A, B, C)
end
end
end
end.
Example for versions Scala 2.7.7-final, Scala 2.8.0-final
This example expands the interactive one with variables input.
import java.io.{BufferedReader, InputStreamReader}
object Main {
def main(args: Array[String]) {
var stdin = new BufferedReader(new InputStreamReader(System.in));
var A = augmentString(stdin.readLine()).toInt;
var B = augmentString(stdin.readLine()).toInt;
var C = augmentString(stdin.readLine()).toInt;
solve(A,B,C);
}
def output(real: Double, imag: Double): String =
if (imag == 0) ""+real
else "("+real+","+imag+")"
def solve(A: Int, B: Int, C: Int)
{ if (A == 0) print("Not a quadratic equation.")
else
{ def D = B*B - 4*A*C;
if (D == 0) print("x = "+output(-B/2.0/A, 0));
else if (D > 0)
print("x1 = "+output((-B+Math.sqrt(D))/2.0/A, 0)+"\nx2 = "+output((-B-Math.sqrt(D))/2.0/A, 0));
else print("x1 = "+output(-B/2/A, Math.sqrt(-D)/2.0/A)+"\nx2 = "+output(-B/2/A, -Math.sqrt(-D)/2.0/A));
}
}
}
Example for versions gc-2010-07-14
When you import several packages, you can put a dot before name of one of them, and use its functions without a package-name prefix, like fmt in this example.
To read a number, one has to read a string from standard input, remove the trailing ‘n’ and convert it into the wanted format. In our case, input variables are integer, but further on we’ll be using them for floating-point calculations. Go doesn’t support implicit type conversions, so it’s better to parse input as float64 (the type of argument for math.Sqrt) right away.
Assignment = is plain one, while := means that the variable on the left side is defined in this line. Note that defined but unused variables count as compilation errors, so you have to use err in some way.
package main
import (
"os"
. "fmt"
"math"
"bufio"
"strconv")
func main() {
in := bufio.NewReader(os.Stdin)
line, err := in.ReadString('\n')
line = line[0 : len(line)-1]
A, err := strconv.Atof64(line)
if (A == 0) {
Print("Not a quadratic equation.")
return
}
line, err = in.ReadString('\n')
line = line[0 : len(line)-1]
B, err := strconv.Atof64(line)
line, err = in.ReadString('\n')
line = line[0 : len(line)-1]
C, err := strconv.Atof64(line)
if err != nil {
Print(err)
}
D := B*B-4*A*C
if (D == 0) {
Printf("x = %f", -B/2/A)
return
}
if (D>0) {
Printf("x1 = %f\nx2 = %f", -B/2/A + math.Sqrt(D)/2/A, -B/2/A - math.Sqrt(D)/2/A)
} else {
Printf("x1 = (%f, %f)\nx2 = (%f, %f)", -B/2/A, math.Sqrt(-D)/2/A, -B/2/A, -math.Sqrt(-D)/2/A)
}
}
Example for versions Lua 5.0.3, Lua 5.1.4
*n specifies that a number has to be read. Everything else is quite evident.
local A = io.read('*n')
if A==0 then
io.write('Not a quadratic equation.')
return
end
local B = io.read('*n')
local C = io.read('*n')
D = B*B-4*A*C
if D==0 then
io.write('x = ', -B/2/A)
else if D>0 then
io.write('x1 = ', (-B+math.sqrt(D))/2/A, '\nx2 = ', (-B-math.sqrt(D))/2/A)
else
io.write('x1 = (', -B/2/A, ',', math.sqrt(-D)/2/A, ')\nx2 = (', -B/2/A, ',', -math.sqrt(-D)/2/A, ')\n')
end
end
Example for versions perl 5.12.1, perl 5.8.8
Note that Perl 6 has no backwards compatibility; this example won’t be valid in Perl 6.
$A = <>;
if ($A == 0) {
print "Not a quadratic equation.";
}
else {
$B = <>;
$C = <>;
$D = $B * $B - 4 * $A * $C;
if ($D == 0) {
print "x = ", -0.5 * $B / $A;
}
else {
if ($D > 0) {
print "x1 = ", 0.5*(-$B + sqrt($D))/$A, "\nx2 = ", 0.5*(-$B - sqrt($D))/$A
}
else {
print "x1 = (", -0.5*$B/$A, ",", 0.5*sqrt(-$D)/$A, ")\nx2 = (", -0.5*$B/$A, ",", -0.5*sqrt(-$D)/$A, ")\n"
}
}
}
Example for versions rakudo-2010.08
This example differs from one in Perl 5 in two major ways: the way user input is read and results are printed, and the way all variables have to be predeclared with my keyword before using them. Note that explicit declaration of variable type stays optional.
my $A = $*IN.get;
if ($A == 0) {
say "Not a quadratic equation.";
}
else {
my $B = $*IN.get;
my $C = $*IN.get;
my $D = $B * $B - 4 * $A * $C;
if ($D == 0) {
say "x = ", -0.5 * $B / $A;
}
else {
if ($D > 0) {
say "x1 = ", 0.5*(-$B + sqrt($D))/$A, "\nx2 = ", 0.5*(-$B - sqrt($D))/$A
}
else {
say "x1 = (", -0.5*$B/$A, ",", 0.5*sqrt(-$D)/$A, ")\nx2 = (", -0.5*$B/$A, ",", -0.5*sqrt(-$D)/$A, ")\n"
}
}
}
Example for versions B-Prolog 7.4, gprolog 1.3.0, swipl 5.6.x
This is an ISO Prolog example, using standard read/1 predicate for reading input. Note that when using read/1, you have to put full stop . after each value you input.
q :- write('A = '),
read(A),
( A = 0, write('Not a quadratic equation');
write('B = '),
read(B),
write('C = '),
read(C),
D is B*B-4*A*C,
( D = 0, write('x = '), X is -B/2/A, write(X);
D > 0, write('x1 = '), X1 is (-B+sqrt(D))/2/A, write(X1), nl, write('x2 = '), X2 is (-B-sqrt(D))/2/A, write(X2);
R is -B/2/A, I is abs(sqrt(-D)/2/A),
write('x1 = ('), write(R), write(', '), write(I), write(')'), nl,
write('x1 = ('), write(R), write(', -'), write(I), write(')')
)
).
Example for versions gprolog 1.3.0
Conditional branching in Prolog is done via ; and , predicates, which correspond to “or” and “and” logical operations. Evaluation starts with first branch (for example, check for A being 0 in line 3); all predicates separated with , are evaluated in row; if all of them evaluate to true, the whole program evaluates to true as well (and further evaluation stops), otherwise the next branch is evaluated.
read_integer is GNU Prolog extension, other implementations don’t have this predicate built-in.
q :- write('A = '),
read_integer(A),
( A = 0, write('Not a quadratic equation');
write('B = '),
read_integer(B),
write('C = '),
read_integer(C),
D is B*B-4*A*C,
( D = 0, write('x = '), X is -B/2/A, write(X);
D > 0, write('x1 = '), X1 is (-B+sqrt(D))/2/A, write(X1), nl, write('x2 = '), X2 is (-B-sqrt(D))/2/A, write(X2);
R is -B/2/A, I is abs(sqrt(-D)/2/A),
write('x1 = ('), write(R), write(', '), write(I), write(')'), nl,
write('x1 = ('), write(R), write(', -'), write(I), write(')')
)
).
q.
Example for versions Python 2.6.5
import math
import sys
A = float(raw_input("A = "))
if A == 0:
print "Not a quadratic equation"
sys.exit()
B = float(raw_input("B = "))
C = float(raw_input("C = "))
D = B * B - 4 * A * C
if D == 0:
print "x =", -B / 2.0 / A
sys.exit()
if D > 0:
print "x1 =", (-B + math.sqrt(D)) / 2.0 / A
print "x2 =", (-B - math.sqrt(D)) / 2.0 / A
else:
print "x1 = (", -B / 2.0 / A, ",", math.sqrt(-D) / 2.0 / A, ")"
print "x2 = (", -B / 2.0 / A, ",", -math.sqrt(-D) / 2.0 / A, ")"
Example for versions PHP 5.3.2
<?php
echo "A = ";
$A = (float) fgets(STDIN);
if ($A == 0) {
die("Not a quadratic equation\n");
}
echo "B = ";
$B = (float) fgets(STDIN);
echo "C = ";
$C = (float) fgets(STDIN);
$D = $B * $B - 4 * $A * $C;
if ($D == 0) {
echo "x = ", -$B / 2.0 / $A, "\n";
die();
}
if ($D > 0) {
echo "x1 = ", (-$B + sqrt($D)) / 2.0 / $A, "\n";
echo "x2 = ", (-$B - sqrt($D)) / 2.0 / $A, "\n";
} else {
echo "x1 = (", -$B / 2.0 / $A, ", ", sqrt(-$D) / 2.0 / $A, ")\n";
echo "x2 = (", -$B / 2.0 / $A, ", ", -sqrt(-$D) / 2.0 / $A, ")\n";
}
?>
Example for versions Mozart 1.4.0
Oz is a strongly typed language, so all type conversions have to be done explicitly. Coefficients are converted in two steps (first to int, next to float) because converting string “1” into a float directly causes an error (“1.” converts into float just fine). ~ denotes unary minus.
functor
import
Application System Open
define
local
A B C D
class TextFile from Open.file Open.text end
StdIn = {New TextFile init(name:stdin)}
in
{System.showInfo "A = "}
A = {Int.toFloat {String.toInt {StdIn getS($)}}}
if A==0 then
{System.showInfo "Not a quadratic equation."}
{Application.exit 0}
end
{System.showInfo "B = "}
B = {Int.toFloat {String.toInt {StdIn getS($)}}}
{System.showInfo "C = "}
C = {Int.toFloat {String.toInt {StdIn getS($)}}}
D = B*B - 4.0*A*C
if D==0.0 then
{System.showInfo "x = "#{Float.toString ~0.5*B/A}}
{Application.exit 0}
end
if D>0.0 then
{System.showInfo "x1 = "#{Float.toString ~0.5*(B-{Sqrt D})/A}}
{System.showInfo "x2 = "#{Float.toString ~0.5*(B+{Sqrt D})/A}}
else
{System.showInfo "x1 = ("#{Float.toString ~0.5*B/A}#","#{Float.toString 0.5*{Sqrt ~D}/A}#")"}
{System.showInfo "x2 = ("#{Float.toString ~0.5*B/A}#","#{Float.toString ~0.5*{Sqrt ~D}/A}#")"}
end
{Application.exit 0}
end
end
Example for versions ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
set A [gets stdin]
if {$A==0} {
puts "Not a quadratic equation.";
return
}
set B [gets stdin]
set C [gets stdin]
set D [expr {$B*$B-4*$A*$C}]
set r [expr {-0.5*$B/$A}]
set i [expr {0.5*sqrt(abs($D))/$A}]
if {$D==0} {
puts "x = $r"
} elseif {$D>0} {
puts "x1 = [expr {$r+$i}]"
puts "x2 = [expr {$r-$i}]"
} else {
puts "x1 = ($r, $i)"
puts "x2 = ($r, [expr {-$i}])"
}
Example for versions Bash 3.0, Bash 4.0.35
Bash itself can’t process floating-point numbers, so to calculate roots we have to use bc.
read A;
if [ $A = 0 ]; then
echo "Not a quadratic equation.";
exit 0;
fi
read B;
read C;
D=$(( ($B)*($B)-4*($A)*($C) ));
#integer math only!
if [ $D = 0 ]; then
echo -n "x = "
echo -e "scale=3\n-0.5*($B)/($A)" | bc
exit 0;
fi
echo $D
if [ $D -gt 0 ]; then
echo -n "x1 = "
echo -e "scale=3\n0.5*(-($B)+sqrt($D))/($A)" | bc
echo -n "x2 = "
echo -e "scale=3\n0.5*(-($B)-sqrt($D))/($A)" | bc
else
echo -n "x1 = ("
echo -e "scale=3\n-0.5*($B)/($A)" | bc
echo -n ", "
echo -e "scale=3\n0.5*sqrt(-($D))/($A)" | bc
echo ")"
echo -n "x2 = ("
echo -e "scale=3\n-0.5*($B)/($A)" | bc
echo -n ", "
echo -e "scale=3\n-0.5*sqrt(-($D))/($A)" | bc
echo ")"
fi
Example for versions boo 0.8.2
A = int.Parse(prompt("A = "))
if A==0 :
print "Not a quadratic equation."
return
B = int.Parse(prompt("B = "))
C = int.Parse(prompt("C = "))
D = B*B-4*A*C
if D==0 :
x = -0.5*B/A
print "x = ${x}"
return
if D>0 :
x1 = 0.5*(-B-System.Math.Sqrt(D))/A
x2 = 0.5*(-B+System.Math.Sqrt(D))/A
print "x1 = ${x1}"
print "x2 = ${x2}"
else :
r = -0.5*B/A
i = 0.5*System.Math.Sqrt(-D)/System.Math.Abs(A)
print "x1 = (${r},${i})"
print "x2 = (${r},-${i})"
Example for versions Ruby 1.9
puts 'A = '
A = gets.chomp.to_f
if (A == 0)
puts 'Not a quadratic equation.'
return
end
puts 'B = '
B = gets.chomp.to_f
puts 'C = '
C = gets.chomp.to_f
D = B*B - 4*A*C
if (D == 0)
puts 'x = '+(-B/2/A).to_s
else
if (D > 0)
puts 'x1 = '+((-B-Math.sqrt(D))/2/A).to_s
puts 'x2 = '+((-B+Math.sqrt(D))/2/A).to_s
else
puts 'x1 = ('+(-B/2/A).to_s+','+(Math.sqrt(-D)/2/A).to_s+')'
puts 'x2 = ('+(-B/2/A).to_s+','+(-Math.sqrt(-D)/2/A).to_s+')'
end
end
Example for versions Web2c 2009
This example uses TeX fixed point arithmetic package fp and it’s macro for solving quadratic equations called \FPqsolve. Note that this macro can find only real roots of equation, and prints “FP error: Quadratic equation does not have a solution” if roots are complex (i.e., non-existent from its point of view).
\input fp.tex
\message{A = }
\read -1 to \a
\message{B = }
\read -1 to \b
\message{C = }
\read -1 to \c
\FPqsolve{\xone}{\xtwo}{\number\a}{\number\b}{\number\c}
$\a x^2+\b x+\c=0$
$x_1=\xone$
$x_2=\xtwo$
\bye
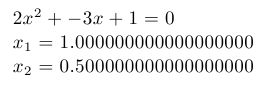
Quadratic equation: document generated by TeX example program
Example for versions Baltie 3
Quadratic equation in Baltie 3
Example for versions Io-2008-01-07
To output several pieces of data in one line, a simple trick is used: these pieces of data form a list, and then the list is concatenated using join command, and the result is printed as one string.
A := File standardInput readLine asNumber;
if(A==0,
"Not a quadratic equation." println;
return;
);
B := File standardInput readLine asNumber;
C := File standardInput readLine asNumber;
D := B*B-4*A*C;
A2 := 2*A;
if(D==0,
list("x = ", (-B/A2) asString) println;
return;
);
sqrtD := D abs sqrt;
if(D>0,
list("x1 = ", ((-B+sqrtD)/A2) asString) join println;
list("x2 = ", ((-B-sqrtD)/A2) asString) join println,
list("x1 = (", (-B/A2) asString, ", ", (sqrtD/A2) asString, ")") join println;
list("x2 = (", (-B/A2) asString, ", ", (-sqrtD/A2) asString, ")") join println;
);
Example for versions Pike 7.8
void main()
{
int A = (int)Stdio.stdin->gets();
if (A == 0)
{
write("Not a quadratic equation.\n");
return 0;
}
int B = (int)Stdio.stdin->gets();
int C = (int)Stdio.stdin->gets();
int D = (B*B-4*A*C);
write(D+"\n");
if (D == 0)
write(sprintf("x = %f\n",-B/2.0/A));
else if (D > 0)
{
write(sprintf("x1 = %f\n", (-B+sqrt(D))/2.0/A));
write(sprintf("x2 = %f\n", (-B-sqrt(D))/2.0/A));
}
else
{
write(sprintf("x1 = (%f, %f)\n", -B/2.0/A, sqrt(-D)/2.0/A));
write(sprintf("x1 = (%f, %f)\n", -B/2.0/A, -sqrt(-D)/2.0/A));
}
}
Example for versions Objeck 2.0.3
use IO;
bundle Default {
class Quadratic {
function : Main(args : String[]) ~ Nil {
A := Console->ReadString()->ToInt();
if (A=0) {
"Not a quadratic equation."->PrintLine();
return;
};
B := Console->ReadString()->ToInt();
C := Console->ReadString()->ToInt();
D := 1.0*(B*B-4*A*C);
if (D=0) {
"x = "->Print();
(0-B/2.0/A)->PrintLine();
};
if (D>0) {
"x1 = "->Print();
((0-B+(D->SquareRoot()))/2.0/A)->PrintLine();
"x2 = "->Print();
((0-B-(D->SquareRoot()))/2.0/A)->PrintLine();
};
if (D<0) {
out := "x1 = (";
out->Append(0-B/2.0/A);
out->Append(",");
out->Append(((D->Abs())->SquareRoot())/2/A);
out->Append(")");
out->PrintLine();
out := "x2 = (";
out->Append(0-B/2.0/A);
out->Append(",");
out->Append(0-((D->Abs())->SquareRoot())/2/A);
out->Append(")");
out->PrintLine();
};
}
}
}
Example for versions gcc 4.2.4
This example requires C99, since it uses complex type introduced in it.
#include <stdio.h>
#include <complex.h>
#include <math.h>
void print(int ind, double complex x) {
printf("x%d = ", ind);
if (fabs(cimag(x)) < 1e-6)
printf("%f\n", creal(x));
else printf("(%f, %f)\n", creal(x), cimag(x));
}
int main() {
double A, B, C;
double D;
printf("A = ");
scanf("%lf", &A);
if (fabs(A)<1E-3) {
printf("Not a quadratic equation\n");
return 1;
}
printf("B = ");
scanf("%lf", &B);
printf("C = ");
scanf("%lf", &C);
A *= 2;
D = B*B-A*C*2.0;
if (fabs(D)<1E-3)
printf("x = %f", creal(-B/A));
else {
print(1, (-B+csqrt(D))/A);
print(2, (-B-csqrt(D))/A);
}
return 0;
}
Example for versions Adobe Flex 3.4
When Main() is called, it contains a small routing to initialize the text fields and display labels.
The example is constructed from four text fields, not counting the clickable button or static text. It takes input from three editable text fields (identified by TextFieldType.INPUT), and places the result in the output text field.
The example may be modified to update the result instantly, but this one requires clicking “Calculate” to get the result.
package
{
import flash.display.SimpleButton;
import flash.display.Sprite;
import flash.events.Event;
import flash.events.MouseEvent;
import flash.text.TextField;
import flash.text.TextFieldType;
/**
* ...
* @author Raymond Martineau
*/
public class Main extends Sprite
{
var tf_a:TextField;
var tf_b:TextField;
var tf_c:TextField;
var tf_result:TextField;
public function Main():void
{
if (stage) init();
else addEventListener(Event.ADDED_TO_STAGE, init);
}
/**
* This function initializes the display elements.
*/
private function init(e:Event = null):void
{
removeEventListener(Event.ADDED_TO_STAGE, init);
// entry point
tf_a = new TextField();
tf_a.text = "1";
tf_a.x = 40;
tf_a.y = 10;
tf_a.height = 20;
tf_a.type = TextFieldType.INPUT;
tf_a.border = true;
this.addChild(tf_a);
tf_b = new TextField();
tf_b.text = "1";
tf_b.x = 40;
tf_b.y = 30;
tf_b.height = 20;
tf_b.type = TextFieldType.INPUT;
tf_b.border = true;
this.addChild(tf_b);
tf_c = new TextField();
tf_c.text = "0";
tf_c.x = 40;
tf_c.y = 50;
tf_c.height = 20;
tf_c.type = TextFieldType.INPUT;
tf_c.border = true;
this.addChild(tf_c);
/**
* If desired, you could add the following line to update
* the calculation whenever the value is changed
*
* tf_a.addEventListener(Event.CHANGE, changed);
* tf_b.addEventListener(Event.CHANGE, changed);
* tf_c.addEventListener(Event.CHANGE, changed);
*
* In this example, it's activated by clicking the calculate button.
*/
var tf:TextField;
tf = new TextField();
tf.text = "A = ";
tf.x = 10;
tf.y = 10;
tf.width = 29;
tf.height = 20;
tf.borderColor = 255;
this.addChild(tf);
tf = new TextField();
tf.text = "B = ";
tf.x = 10;
tf.y = 30;
tf.width = 29;
tf.height = 20;
this.addChild(tf);
tf = new TextField();
tf.text = "C = ";
tf.x = 10;
tf.y = 50;
tf.width = 29;
tf.height = 20;
this.addChild(tf);
var btn:TextField = new TextField();
btn.x = 40
btn.y = 80
btn.width = 80
btn.height = 20
btn.text = "Calculate"
btn.border = true;
btn.backgroundColor = 0xcccccc;
btn.background = true;
btn.selectable = false;
this.addChild(btn);
btn.addEventListener(MouseEvent.CLICK, changed);
tf_result = new TextField();
tf_result.x = 10;
tf_result.y = 110;
tf_result.width = 400;
this.addChild(tf_result);
updateResult();
}
private function changed(e:Event = null)
{
updateResult();
}
private function updateResult()
{
var a:Number, b:Number, c:Number, d:Number;
a = Number(tf_a.text); b = Number(tf_b.text); c = Number(tf_c.text);
d = b * b - 4 * a * c;
if (a == 0)
{
tf_result.text = "Not a quadratic equation";
}
else if (d == 0)
{
tf_result.text = "One root: " + ( -b / (2 * a));
}
else if (d>0)
{
tf_result.text = "Two roots: " + (( -b + Math.sqrt(d)) / (2*a)) + ", " + (( -b - Math.sqrt(d)) / (2*a));
} else if (d < 0)
{
var e:Number = -b / 2 * a;
var f:Number = Math.sqrt( -d) / 2 * a;
if (f < 0) f = -f;
tf_result.text = "Two roots: (" + e + ", " + f + "), (" + e + " - " + f + ")";
}
return 0;
}
}
}
Example for versions GNU Octave 3.2.3
Octave is suited for numeric computations, so it has built-in methods of solving typical problems, including finding the roots of a polynomial. To do this one can call roots function for a vector of polynomial coefficients listed in order of descending powers (so the coefficient at the highest power is listed first).
roots([2 -3 1])
Example for versions Clojure 1.0.0, Clojure 1.1.0
(defn solve-quadratic [a b c]
(if (= a 0)
"Not a quadratic equation."
(let [D (- (* b b) (* 4 a c))
k1 (- 0 b)
k2 (* 2 a)]
(if (= D 0)
(str "x = " (/ k1 k2))
(if (> D 0)
(let [k3 (Math/sqrt D)]
(str (str "x1 = " (/ (+ k1 k3) k2) (str "\nx2 = " (/ (- k1 k3) k2)))))
(let [k3 (Math/sqrt (- 0 D))]
(str (str (str (str "x1 = (" (/ k1 k2)) (str ", " (/ k3 k2))) ")\nx2 = (") (str (str (/ k1 k2) ", ") (str (- 0 (/ k3 k2)) ")") ))
))))))
(import '(java.util Scanner))
(def scan (Scanner. *in*))
(def a (.nextInt scan))
(def b (.nextInt scan))
(def c (.nextInt scan))
(println (solve-quadratic a b c))
Example for versions Seed7 2012-01-01
$ include "seed7_05.s7i";
include "float.s7i";
include "math.s7i";
const proc: main is func
local
var float: a is 0.0;
var float: b is 0.0;
var float: c is 0.0;
var float: d is 0.0;
begin
readln(a);
if a = 0.0 then
writeln("Not a quadratic equation.");
else
readln(b);
readln(c);
d := b ** 2 - 4.0 * a * c;
if d = 0.0 then
writeln("x = " <& (-b / 2.0 / a));
else
if d > 0.0 then
writeln("x1 = " <& ((-b + sqrt(d)) / 2.0 / a));
writeln("x2 = " <& ((-b - sqrt(d)) / 2.0 / a));
else
writeln("x1 = (" <& (-b / 2.0 / a) <& "," <& (sqrt(-d) / 2.0 / a) <& ")");
writeln("x2 = (" <& (-b / 2.0 / a) <& "," <& (-sqrt(-d) / 2.0 / a) <& ")");
end if;
end if;
end if;
end func;
Example for versions Falcon 0.9.6.6
a = int(input())
if a == 0
printl("Not a quadratic equation.")
exit()
end
b = int(input())
c = int(input())
d = b ** 2 - 4 * a * c
if d == 0
printl("x = " + (-b / 2.0 / a))
else
if d > 0
printl("x1 = " + ((-b + d**0.5) / 2.0 / a))
printl("x2 = " + ((-b - d**0.5) / 2.0 / a))
else
printl("x1 = (" + (-b / 2.0 / a) + "," + ((-d)**0.5 / 2.0 / a) + ")")
printl("x2 = (" + (-b / 2.0 / a) + "," + (- ((-d)**0.5 / 2.0 / a)) + ")")
end
end
Example for versions iconc 9.4
procedure main ()
A := read();
if A = 0 then {
write("Not a quadratic equation.");
return;
}
B := read();
C := read();
D := B*B - 4*A*C;
if D = 0 then {
write("x = ", -B/2/A);
return;
}
if D > 0 then {
write("x1 = ", (-B+sqrt(D))/2/A);
write("x2 = ", (-B-sqrt(D))/2/A);
} else {
write("x1 = (", -B/2/A, ",", sqrt(-D)/2/A, ")");
write("x2 = (", -B/2/A, ",", -sqrt(-D)/2/A, ")");
}
end
Example for versions Factor 0.94
Word quadratic-equation takes coefficients of the equation as input and prints the solution while returning nothing. Note that this word is declared using token :: instead of : used in most cases; this means that within it lexically scoped variables can be used, in this case parameters a, b and c as well as local variables d, x0 and sd bound by :> operator. Such variables can be loaded on the stack using their names. Words and operators which process lexically scoped variables are available in dictionary locals.
Factor provides a built-in data type for complex numbers; whenever the discriminant is negative, its square root will be of type complex. In this case complex roots are printed using words real-part and imaginary-part which extract corresponding parts of a number.
readln reads a string from input stream (till the end of line), and string>number (from math.parser dictionary) converts a string to a floating-point number.
USING: formatting io kernel locals math math.functions math.parser ;
IN: quadratic-example
:: quadratic-equation ( a b c -- )
a 0 =
[ "Not a quadratic equation." printf ]
[ b sq a c * 4 * - :> d
b neg a 2 * / :> x0
d sqrt a 2 * / :> sd
d 0 =
[ x0 "x = %f\n" printf ]
[ d 0 >
[ x0 sd + x0 sd - "x1 = %f\nx2 = %f\n" printf ]
[ x0 sd + [ real-part ] [ imaginary-part ] bi "x1 = (%f, %f)\n" printf
x0 sd - [ real-part ] [ imaginary-part ] bi "x2 = (%f, %f)\n" printf ]
if
]
if
]
if ;
readln string>number
readln string>number
readln string>number
quadratic-equation
Example for versions Oracle 11g SQL
declare
A number := '&A';
B number := '&B';
C number := '&C';
D number := B * B - 4 * A * C;
begin
if A = 0 then
dbms_output.put_line('Not a quadratic equation.');
return;
end if;
if D = 0 then
dbms_output.put_line('x = ' || to_char(-B/2/A));
elsif D > 0 then
dbms_output.put_line('x1 = ' || to_char((-B-sqrt(D))/2/A));
dbms_output.put_line('x2 = ' || to_char((-B+sqrt(D))/2/A));
else
dbms_output.put_line('x1 = (' || to_char(-B/2/A) || ', ' || to_char(sqrt(-D)/2/A) || ')');
dbms_output.put_line('x2 = (' || to_char(-B/2/A) || ', ' || to_char(-sqrt(-D)/2/A) || ')');
end if;
end;
Example for versions loljs 1.1
HAI
HOW DUZ I SQRT X
I HAS A X_N ITZ 10
I HAS A LIMIT ITZ 100
I HAS A COUNTER ITZ 0
IM IN YR LOOP UPPIN YR COUNTER WILE COUNTER SMALLR THAN LIMIT
I HAS A TERM ITZ QUOSHUNT OF X AN X_N
TERM R SUM OF X_N AN TERM
TERM R QUOSHUNT OF TERM AN 2
X_N R TERM
IM OUTTA YR LOOP
FOUND YR X_N
IF U SAY SO
I HAS A AC
GIMMEH AC
AC IS NOW A NUMBR
BOTH SAEM AC AN 0, O RLY?
YA RLY
VISIBLE "Not a quadratic equation."
NO WAI
I HAS A BC
GIMMEH BC
BC IS NOW A NUMBR
I HAS A CC
GIMMEH CC
CC IS NOW A NUMBR
I HAS A D ITZ DIFF OF PRODUKT OF BC AN BC AN PRODUKT OF 4 AN PRODUKT OF AC AN CC
BOTH SAEM D AN 0, O RLY?
YA RLY
VISIBLE SMOOSH "x = " QUOSHUNT OF BC AN PRODUKT OF -2 AN AC
NO WAI
BOTH SAEM 0 AN SMALLR OF 0 AN D, O RLY?
YA RLY
VISIBLE SMOOSH "x1 = " QUOSHUNT OF SUM OF BC AN SQRT D AN PRODUKT OF -2 AN AC
VISIBLE SMOOSH "x2 = " QUOSHUNT OF DIFF OF BC AN SQRT D AN PRODUKT OF -2 AN AC
NO WAI
D R PRODUKT OF D AN -1
VISIBLE SMOOSH "x1 = (" QUOSHUNT OF BC AN PRODUKT OF -2 AN AC ", " QUOSHUNT OF SQRT D AN PRODUKT OF -2 AN AC ")"
VISIBLE SMOOSH "x2 = (" QUOSHUNT OF BC AN PRODUKT OF -2 AN AC ", " QUOSHUNT OF SQRT D AN PRODUKT OF 2 AN AC ")"
OIC
OIC
OIC
KTHXBYE
Example for versions Wolfram Mathematica 8.0.4
After accepting user input we define variable y which is a quadratic equation with the given coefficients. Since x is not defined yet, it stays a variable — for example, Print[y] will output the notation of the equation c + b x + a x^2 (with c, b and a replaced with values entered by the user). Reduce calculates the values of the variables which satisfy the condition “equation value equals zero”.
a = Input["Input a", 0];
b = Input["Input b", 0];
c = Input["Input c", 0];
y = a*x^2 + b*x + c;
Print[Reduce[y == 0]];
Example for versions Dyalog APL 13.1
This code defines a named D-function which accepts equation coefficients as a single argument (a three-element array) and returns equation solution. First the argument is split into separate coefficients (N⊃⍵ picks Nth element of the array) and they are assigned names. After this first coefficient and discriminant are checked — if one of them is zero, the function returns a special value. Finally, non-zero discriminant is processed with the same code regardless of its sign due to the fact that APL has built-in complex numbers datatype. A function call
solve 1 0 2
will return:
0J1.4142135623730951 0J¯1.4142135623730951
(J is a separator between real and imaginary parts of the number, and ¯ — is a “high” minus, used for input/output of negative numbers).
Note that this code is not typical for APL due to conditional branching use as well as limiting possible arguments to a one-dimensional array of three elements.
solve←{A←0⊃⍵ ⋄ B←1⊃⍵ ⋄ C←2⊃⍵ ⋄ A=0:'Not a quadratic equation.' ⋄ D←(B*2)-4×A×C ⋄ D=0:-0.5×B÷A ⋄ ((-B-D*0.5), -B+D*0.5)×0.5÷A}
Example for versions Nimrod 0.8.8
from math import sqrt
from strutils import parseFloat
var A = parseFloat(readLine(stdin))
if A == 0.0:
echo "Not a quadratic equation."
else:
var B = parseFloat(readLine(stdin))
var C = parseFloat(readLine(stdin))
var D = B * B - 4.0 * A * C
if D == 0.0:
echo "x = ", -0.5 * B / A
elif D > 0.0:
echo "x1 = ", -0.5 * (B - sqrt(D)) / A
echo "x2 = ", -0.5 * (B + sqrt(D)) / A
else:
echo "x1 = (", -0.5 * B / A, ", ", 0.5 * sqrt(-D) / A, ")"
echo "x2 = (", -0.5 * B / A, ", ", -0.5 * sqrt(-D) / A, ")"
Example for versions VBScript 5.7, VBScript 5.8
Function GetInt()
Input = WScript.StdIn.ReadLine
If not IsNumeric(Input) Then
WScript.Echo "Coefficient is not a number."
WScript.Quit
End If
GetInt = CInt(Input)
End Function
A = GetInt()
If A = 0 Then
WScript.Echo "Not a quadratic equation."
WScript.Quit
End If
B = GetInt()
C = GetInt()
D = B * B - 4 * A * C
p1 = -B / 2.0 / A
p2 = Sqr(Abs(D)) / 2.0 / A
If D = 0 Then
WScript.Echo "x = " & p1
Else
If D > 0 Then
WScript.Echo "x1 = " & (p1 + p2)
WScript.Echo "x2 = " & (p1 - p2)
Else
WScript.Echo "x1 = (" & p1 & ", " & p2 & ")"
WScript.Echo "x2 = (" & p1 & ", " & -p2 & ")"
End If
End If
Example for versions guile 1.8.5
begin is used to execute several commands in row.
(define A (read))
(define B (read))
(define C (read))
(define D (- (* B B) (* 4 A C)))
(if (= A 0)
(display "Not a quadratic equation.")
(begin
(define k1 (/ B -2 A))
(define k2 (/ (sqrt (abs D)) 2 A))
(if (= D 0)
(begin (display "x = ") (display k1))
(if (> D 0)
(begin (display "x1 = ") (display (+ k1 k2)) (newline) (display "x2 = ") (display (- k1 k2)))
(begin (display "x1 = (") (display k1) (display ", ") (display k2) (display ")") (newline)
(display "x2 = (") (display k1) (display ", ") (display (- k2)) (display ")"))))))
Example for versions gfortran 4.5.0
This example uses built-in complex data type.
program Quadratic
integer a, b, c
real d, p1, p2
complex cp2
read (*, *) a
if (a.eq.0) then
write (*, *) "Not a quadratic equation"
stop
end if
read (*, *) b
read (*, *) c
d = b * b - 4 * a * c
p1 = - b / 2.0 / a
if (abs(d) < 1.0e-9) then
write (*, "(A, F8.3)") "x = ", p1
elseif (d > 0) then
p2 = sqrt(d) / 2.0 / a
write (*, "(2(A, F8.3))") "x1 = ", p1 + p2, char(13)//char(10)//"x2 = ", p1 - p2
else
cp2 = sqrt(cmplx(d)) / 2.0 / a
write (*, "(2(A, F8.3, F8.3), A)") "x1 = (", p1 + cp2, ")"//char(13)//char(10)//"x2 = (", p1 - cp2, ")"
end if
end
Example for versions Dart 1.1.1
import 'dart:io';
import 'dart:math' show sqrt;
int readInt() {
String input = stdin.readLineSync();
return int.parse(input);
}
main() {
int A, B, C;
try {
A = readInt();
B = readInt();
C = readInt();
}
on FormatException {
print("Coefficient is not a number.");
return;
}
if (A == 0) {
print("Not a quadratic equation.");
return;
}
int D = B * B - 4 * A * C;
double p1 = - B / 2.0 / A;
double p2 = sqrt(D.abs()) / 2.0 / A;
if (D == 0) {
print("x = $p1");
} else {
if (D > 0) {
print("x1 = ${p1 + p2}");
print("x2 = ${p1 - p2}");
} else {
print("x1 = ($p1, $p2)");
print("x2 = ($p1, ${-p2})");
}
}
}
Example for versions OCaml 3.11
ocaml quadratic_equation.ml 3. 5. 2.
let square x = x *. x;;
let delta a b c = ( square b-. (4. *. a *. c ));;
let solve a b c =
if a=0.
then Printf.printf "Not a quadratic equation\n"
else
if delta a b c >= 0.
then
let x1=( -.b +. sqrt(delta a b c )) /. (2. *. a)
and x2= (-.b -. sqrt(delta a b c )) /. (2. *. a)
in
Printf.printf "x1 =%.5f x2=%.5f \n" x1 x2
else
let x= (-.b /. (2. *. a))
and i= sqrt(4. *. a *. c -. square b) /. (2. *. a)
in Printf.printf "x+ =%.5f+i%.5f x-=%.5f-i%.5f \n" x i x i
;;
let () =
solve (float_of_string Sys.argv.(1))( float_of_string Sys.argv.(2) )(float_of_string Sys.argv.(3))
Example for versions Wouter's FALSE 1.2.CF
This example is identical to the one written for Morphett’s FALSE, except that in Wouter’s FALSE end of input is signaled by end of line character, which is used for breaking the loop. Besides, % in the end of the code deletes the last leftover value from the stack.
1_s: ^
[$10=~]
[ $$ 96> \123\> & [32-]?
$$ 64> \91\> & $l: [s;~[32+]? , 0s:]? l;~[1_s: %]?
^]
#
%
Example for versions Microsoft SQL Server 2005, Microsoft SQL Server 2008 R2, Microsoft SQL Server 2012
SELECT dbo.quadratic_equation(1,2,1)
SELECT dbo.quadratic_equation(1,2,3)
CREATE FUNCTION quadratic_equation (@a FLOAT
,@b FLOAT
,@c float )
RETURNS varchar (100)
AS
BEGIN
DECLARE @ret varchar(100);
declare @delta float ;
declare @denom float ;
select @delta=(POWER(@b,2)-4*@a*@c);
select @denom=(2*@a);
if (@delta>=0)
BEGIN
DECLARE @x12 FLOAT;
SELECT @x12=((-@b+SQRT(@delta))/@denom);
SELECT @ret='x1='+ CONVERT(varchar(100),@x12 )
+' x2='+ CONVERT(varchar(100),@x12 )
END
ELSE
BEGIN
DECLARE @nat FLOAT;
DECLARE @imm FLOAT;
SELECT @nat=((-@b)/@denom);
SELECT @imm=((SQRT(-@delta))/@denom);
SELECT @ret='x1='+ CONVERT(varchar(100),@nat)+'+i'+CONVERT(varchar(100),@imm )
+' x2='+ CONVERT(varchar(100),@nat)+'-i'+CONVERT(varchar(100),@imm )
end
RETURN @ret ;
END;
Example for versions Snap! 4.0
In Snap! block join conveniently allows to concatenate arbitrary number of arguments.
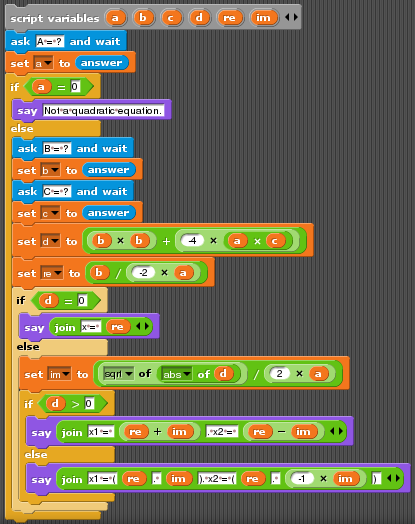
Quadratic equation in Snap!