TeX

Appeared in:
1978
Paradigm:
Typing discipline:
File extensions:
.tex
Versions and implementations (Collapse all | Expand all):
Programming language

TeX is a typesetting system designed and mostly written by Donald Knuth.

TeX commands commonly start with a backslash and are grouped with curly braces. Almost all of TeX’s syntactic properties can be changed on the fly which makes TeX input hard to parse by anything but TeX itself. Many commands, including most user-defined ones, are expanded on the fly until only unexpandable tokens remain which get executed. Expansion itself is practically side-effect free. Tail recursion of macros takes no memory, and if-then-else constructs are available.

While being a typesetting system TeX also has powerful macro abilities that make it a Turing-complete programming language.

Elements of syntax:

Inline comments %
Variable assignment varname = value
Block { ... }

TeX logo
TeX logo

Links:

Examples:

Hello, World!:

Example for versions Web2c 2009 
Hello, World!
\bye

Quadratic equation:

Example for versions Web2c 2009

This example uses TeX fixed point arithmetic package fp and it’s macro for solving quadratic equations called \FPqsolve. Note that this macro can find only real roots of equation, and prints “FP error: Quadratic equation does not have a solution” if roots are complex (i.e., non-existent from its point of view). 

\input fp.tex

\message{A = }
\read -1 to \a
\message{B = }
\read -1 to \b
\message{C = }
\read -1 to \c

\FPqsolve{\xone}{\xtwo}{\number\a}{\number\b}{\number\c}

$\a x^2+\b x+\c=0$

$x_1=\xone$

$x_2=\xtwo$
\bye

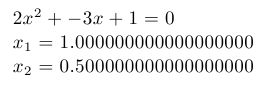
Quadratic equation: document generated by TeX example program
Quadratic equation: document generated by TeX example program

Factorial:

Example for versions Web2c 2009

This example uses iterative factorial definition.

Note that \factorial macro has to use double curly brackets because it has loop that is used inside other loop.

Also only factorials up to 12 are handled. For bigger numbers TeX throws “Arithmetic overflow” error. 

\newcount\n \newcount\p \newcount\m

\def\factorial#1{{\m=#1\advance\m by 1
\n=1
\p=1
\loop\ifnum\n<\m \multiply\p by \n \advance\n by 1 \repeat\number\p}}

\def\printfactorials#1{\m=#1\advance\m by 1
\n=0
\loop\ifnum\n<\m \hfil\break\number\n! = \factorial{\n} \advance\n by 1 \repeat}

\printfactorials{12}
\bye

Fibonacci numbers:

Example for versions Web2c 2009

This example uses iterative process to calculate Fibonacci numbers.

Note that \fibonacci macro has to use double curly brackets because it has loop that is used inside other loop. 

\newcount\n \newcount\np \newcount\npp \newcount\m \newcount\f

\def\fibonacci#1{{\ifnum #1<3 1\else
\np=1\npp=1\m=3
\loop\ifnum\m<#1\f=\npp\npp=\np\advance\np by\f\advance\m by 1\repeat
\f=0\advance\f by\np\advance\f by\npp
\number\f\fi}}

\def\printfibonacci#1{\m=#1\advance\m by 1
\n=1
\loop\ifnum\n<\m\fibonacci{\n}, \advance\n by 1\repeat...}

\printfibonacci{16}
\bye