Web2c

Implementation of programming language TeX

Web2c is an implementation of TeX which translates the original WEB sources written by Donald Knuth into C, so they can be readily compiled on modern systems.

The original TeX-to-C implementation was created by Tomas Rokicki 1987, based on change files for TeX under Unix, which were primarily the original work of Howard Trickey and Pavel Curtis. After several years the name was changed to Web-to-C, and in 1990 the shorter name Web2c became commonly used.

Now Web2c is maintained as part of the TeX Live distribution.

Links:

Examples:

Hello, World!:

Example for versions Web2c 2009 
Hello, World!
\bye

Quadratic equation:

Example for versions Web2c 2009

This example uses TeX fixed point arithmetic package fp and it’s macro for solving quadratic equations called \FPqsolve. Note that this macro can find only real roots of equation, and prints “FP error: Quadratic equation does not have a solution” if roots are complex (i.e., non-existent from its point of view). 

\input fp.tex

\message{A = }
\read -1 to \a
\message{B = }
\read -1 to \b
\message{C = }
\read -1 to \c

\FPqsolve{\xone}{\xtwo}{\number\a}{\number\b}{\number\c}

$\a x^2+\b x+\c=0$

$x_1=\xone$

$x_2=\xtwo$
\bye

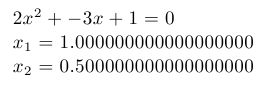
Quadratic equation: document generated by TeX example program
Quadratic equation: document generated by TeX example program

Factorial:

Example for versions Web2c 2009

This example uses iterative factorial definition.

Note that \factorial macro has to use double curly brackets because it has loop that is used inside other loop.

Also only factorials up to 12 are handled. For bigger numbers TeX throws “Arithmetic overflow” error. 

\newcount\n \newcount\p \newcount\m

\def\factorial#1{{\m=#1\advance\m by 1
\n=1
\p=1
\loop\ifnum\n<\m \multiply\p by \n \advance\n by 1 \repeat\number\p}}

\def\printfactorials#1{\m=#1\advance\m by 1
\n=0
\loop\ifnum\n<\m \hfil\break\number\n! = \factorial{\n} \advance\n by 1 \repeat}

\printfactorials{12}
\bye

Fibonacci numbers:

Example for versions Web2c 2009

This example uses iterative process to calculate Fibonacci numbers.

Note that \fibonacci macro has to use double curly brackets because it has loop that is used inside other loop. 

\newcount\n \newcount\np \newcount\npp \newcount\m \newcount\f

\def\fibonacci#1{{\ifnum #1<3 1\else
\np=1\npp=1\m=3
\loop\ifnum\m<#1\f=\npp\npp=\np\advance\np by\f\advance\m by 1\repeat
\f=0\advance\f by\np\advance\f by\npp
\number\f\fi}}

\def\printfibonacci#1{\m=#1\advance\m by 1
\n=1
\loop\ifnum\n<\m\fibonacci{\n}, \advance\n by 1\repeat...}

\printfibonacci{16}
\bye