j602
Version of implementation j602 of programming language Jj602
Examples:
Hello, World! - J (92):
1!:2 is the dyadic foreign conjunction for writing text, the left argument is the string to be written and the right argument specifies the file number, a file number 2 indicates that the text is to be written to the screen.
Alternatively we can use currying to convert the dyadic write conjunction into a monadic conjunction using the bond (&) operator and assign it to a named print function.
The printf library may also be used to print text to the screen.
'Hello, World!' 1!:2]2
print=: 1!:2&2
print 'Hello, World!'
load 'printf'
'' printf 'Hello, World!\n'
Fibonacci numbers - J (103):
This example uses the recursive definition of Fibonacci numbers. @.(agenda) is a higher order dyadic function taking an array of functions(a gerund, created by tying together individual functions using the tie conjunction represented by a back-tick character) on the left and a function on the right that computes the index of the function in the function array(gerund) to be applied on the called argument.
The general call to agenda:
f1`f2@.g x
The function g is used to calculate an index using the argument x, this index is then used to select the function to be applied from the left argument of agenda, the function array. The function that is selected is then applied to the original argument x.
In the case of the above Fibonacci function, applying the semantics of the agenda function we get a function which checks whether its argument is less than two, if it is then 1 is returned otherwise the formal recursive calculation of the Fibonacci number is called on the argument.
load 'printf'
fibr=: 1:`(-&2 +&$: -&1)@.(2&<)"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibr >: i.16
Fibonacci numbers - J (104):
This example uses iterative definition of Fibonacci numbers.
load 'printf'
fibi=: 3 : '(,+/@(_2&{.))^:y(0 1)'
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf }.fibi 15
Fibonacci numbers - J (105):
This example uses Binet’s formula.
g =: -: >: %:5 is equivalent to g =: 0.5 * (1 + 5 ^ 0.5) and assigns name g to value of golden ratio. %: extracts square root of the number, >: increments the number, -: divides the number by two. Operations are done from right to left, unless there are no parenthesis in the formula.
fibb=: (%:5) %~ g&^ -- (1-g)&^ is equivalent to fibb =: (0.2 ^ 0.5) * (g &^ -- (1-g) &^); this defines a formula for F(n) given the value of n. %~ is division, with dividend and divisor swapped.
i.16 generates numbers from 0 to 15, inclusive.
load 'printf'
g=: -: >: %:5
fibb=: (%:5) %~ g&^ - (1-g)&^
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibb 1+i.16
Factorial - J (106):
This example implements three methods of calculating factorial. fact represents a factorial function which generates the first n integers as an array and multiplies them together. factr represents the recursive definition. ! is the built-in factorial function.
load 'printf'
fact=: [: */ [: >: i.
factr=: 1:`(]*$:@<:)@.*
'!%d = %d' printf (,"0 fact) i.17x
'!%d = %d' printf (,"0 factr) i.17x
'!%d = %d' printf (,"0 !) i.17x
Quadratic equation - J (195):
Run calc'' in an interactive J session after loading the file. The function calc2 calculates the roots of the equation using J’s built in root function(p.).
print=: 1!:2&2
read=: 3 : '". 1!:1[1'
a=: 0&{ [ b=: 1&{ [ c=: 2&{
d=: *:@b - [:*/4,a,c
roots=: ([:-b%2*a)`(+:@a %~ (,-)@%:@d + -@b)@.([:*/*)
input=: 3 : 0
A=: read'' [ print 'A = '
B=: read'' [ print 'B = '
C=: read'' [ print 'C = '
)
calc=: 3 : 0
input''
if. A=0 do. print 'Not a quadratic equation' throw. end.
rt=: roots A,B,C
disp rt
)
disp=: 3 : 0
form=: ((('('&,)@":@{.,',',(,&')')@":@}.)@+.)`":@.(=+)
if. 1<# ~.y do.
print 'x1 = ', form 0{y
print 'x2 = ', form 1{y
else.
print 'x = ', form {.y
end.
)
calc2=: 3 : 0
input''
rt=: ;}.p.|.A,B,C
disp rt
)
Fibonacci numbers - J (235):
Maxtrix closed form
load 'printf'
mat =: 1 1,.1 0
fibm=: 3 : '1 { , mat&(+/ . *)^:y mat'"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibm >:i.16
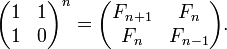
Fibonacci Matrix Closed Form
CamelCase - J (304):
alpha is the set of upper and lower case alphabetic characters.
camel is an explicit solution to the problem, meaning that the variables to the function(y) are mentioned in the function body. The strategy used is to calculate the indices(i) of the alphabetic characters from the bit vector(b) which represents whether or not a character is alphabetic. The function then takes the leading index of each interval of these alphabetic characters and uses that to replace them by their capitalized form. Finally the string is sieved using b so that it contains only the alphabetic characters.
camel2 is a tacit definition, it cuts the input string at the delimiters(non-alphabetic characters), leaving a collection of boxed strings. The leading character of each of these boxed strings is then capitalized and they are all concatenated together forming the final result.
camel3 takes advantage of the built-in libraries, a regular expression is used to split the string into boxed strings, each of these is then capitalized and concatenated.
In all three functions the input is first converted to lower case.
check can be used to ensure that all the functions produce equivalent output.
alpha=: a.{~,65 97+/i.26
camel=: 3 : 0
y=. tolower y
i=. I. (> 0,}:) b=. y e. alpha
(b # toupper@(i&{) i} ]) y
)
isalpha=: e.&alpha
capital=: (toupper@{.,}.)^:(1<:#)
format =: [: ,&' ' tolower
case =: [: ; [: capital&.> ] <;._2~ [: -. isalpha
camel2 =: case@format
require'regex text'
camel3=: [: ; [: capitalize&.> [: '[a-zA-Z]+'&rxall tolower
check=: [: ,. camel;camel2;camel3
Comments
]]>blog comments powered by Disqus
]]>